Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.7 - Ex. 64
- Use um sistema algébrico computacional para calcular , onde
- Determine uma expressão para , expressando, primeiramente, em frações parciais.
Passo 1
E aí, galerinha!
Nesse problema foi dada a função
E nosso objetivo é determinar usando um sistema algébrico e depois refazer os cálculos separando em frações parciais.
Parece complicado?
Para resolver esse problema vamos usar uma plataforma muito popular no meio que é o Symbolab, mas fique a vontade para usar a plataforma que preferir, o importante é chegar no mesmo resultado.
Vamos copiar a função no programa e pedir a derivada de terceira ordem.
Depois vamos separar a função em frações parciais e calcular a derivada de terceira ordem do resultado.
Veja só!
Passo 2
Usando o site Symolab, vamos derivar diretamente três vezes diretamente a função, para obter :
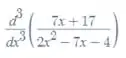
Perceba que a plataforma nos deu os passos que ela seguiu para obter o resultado... primeiramente ela calculou a derivada de primeira ordem.
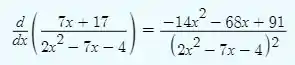
Depois derivou o resultado para obter a derivada de segunda ordem
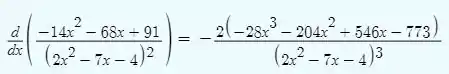
E por fim, derivou o resultado para obter a derivada de terceira ordem.
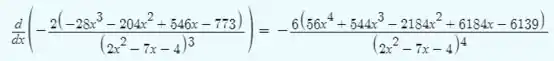
Ou seja, vemos que
Tranquilo até aqui?
Passo 3
Vamos usar o Symbolab mais uma vez para separar a função em frações parciais
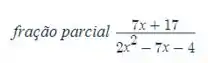
Novamente a plataforma nos deu um passo a passo, mas o resultado foi
Ou seja
Calculando a derivada de ordem três da função em frações parciais, vamos obter
Ou seja...
E aí! entendeu tudo? Responde Aí!