Um carro inicia do repouso, e o gráfico de sua posição está mostrado na figura, onde é medida em pés e , em segundos. Use-o para fazer o gráfico da velocidade e estime a aceleração em segundos do gráfico da velocidade. Então esboce um gráfico da função da aceleração.
Passo 1
Fala aí, tudo belezinha com você?
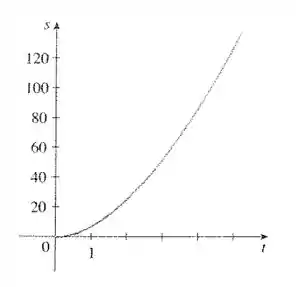
Bom, essa questão deu pra gente o seguinte gráfico:
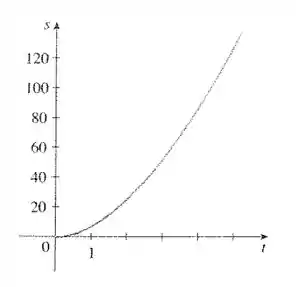
E disse que é o gráfico da posição de um carro que se inicia do repouso.
Devemos usar esse gráfico para fazer o gráfico da velocidade e estimar a aceleração em segundos do gráfico da velocidade.
E depois, também devemos esboçar um gráfico da função da aceleração.
Para fazer tudo isso devemos lembrar que a velocidade é a taxa de variação da posição.
Sendo assim, é a inclinação do gráfico de .
Vamos então analisar a inclinação do gráfico de em alguns pontos, para tentar esboçar o gráfico de .
Depois disso, sabemos também que a aceleração é a taxa de variação da velocidade,
então tendo o gráfico da velocidade basta olhar sua inclinação em um ponto para saber o valor da aceleração naquele ponto (mesmo processo que usamos para achar a velocidade a partir da posição).
Então, partiu resolver tudo isso!!!
Passo 2
Vamos traçar tangentes à curva de em alguns pontos para saber a inclinação. A inclinação da reta começa horizontal ( e vai aumentando. O desenho mostra as tangentes que traçamos.
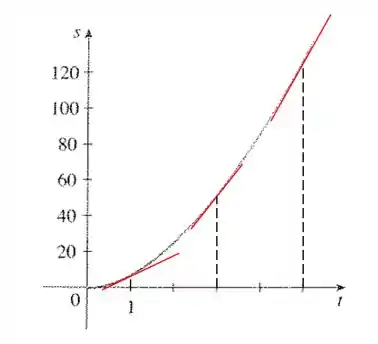
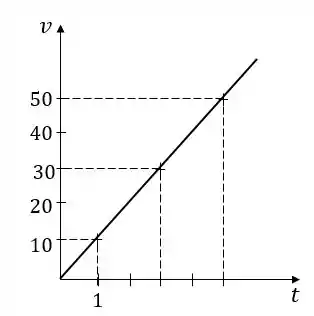
Vamos calcular aproximadamente os valores de para esses três pontos (.
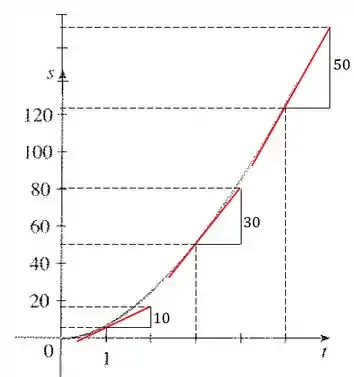
Com isso, temos:
Marcando esses pontos num plano cartersiano, vemos que parece ser uma reta:
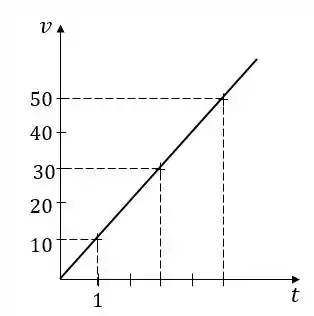
Passo 3
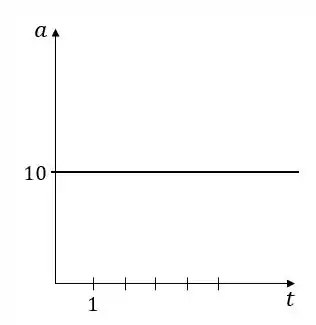
Como o gráfico da velocidade é uma reta, a aceleração, que é a inclinação do gráfico da velocidade pelo tempo, será constante. A aceleração para será a mesma que para todos os outros tempos. Vamos calcular a aceleração dividindo a variação da velocidade pela variação do tempo de 0 a 5 segundos:
Então o gráfico da aceleração é uma reta horizontal:
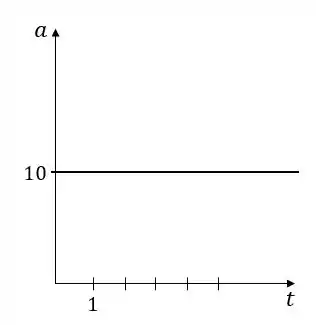
Resposta