Um pedreiro dispõe de uma escada de 3 m de comprimento e precisa, com ela, acessar o telhado de uma casa. Sabendo que o telhado se apoia sobre uma parede de 4 m de altura e que o menor ângulo entre a escada e a parede para a escada não cair é 20°, a que altura do chão ele deve apoiar a escada?
Passo 1
E aí pessoal, beleza?
Pelo enunciado temos a seguinte situação:
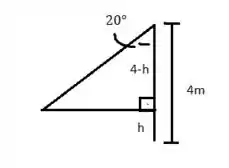
Pela tabela da página 309 temos que e pelo enunciado que o tamanho da escada é 3 m.
Passo 2
Assim, podemos fazer:
Fechou! Vamos pra próxima?