Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.7 - Ex. 75

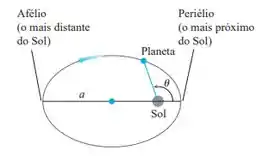
Periélio e afélio. Um planeta dá uma volta em torno do Sol em uma elipse cujo semieixo maior tem comprimento a. (Veja a figura a seguir.)

a. Mostre que r = a ( 1 - e ) quando o planeta está mais próximo do Sol e que r = a ( 1 + e ) quando o planeta está mais distante do Sol.

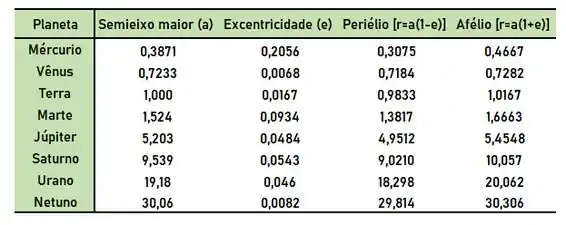
b. Utilize os dados da tabela no Exercício 76 para determinar o quão próximo cada um dos planetas em nosso sistema solar chega do Sol e o quão distante cada planeta chega do Sol.

Passo 1

Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?

Neste problema vamos nos basear na figura dada para deduzir as equações do raio da elipse que descreve o movimento do planeta no momento do periélio e o do afélio. Em seguida, vamos calcular estes raios para os planetas do sistema solar com base na medidas de a e e .

Bora lá?

Passo 2

(a) O planeta está mais próximo do sol no periélio, então da figura, temos:

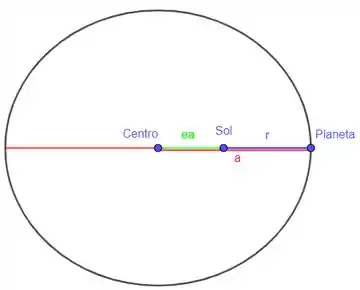
Note que a distância r entre o planeta e o sol é dada por:

r = a - e a

r = a ( 1 - e )

O planeta está mais próximo do sol no periélio, então da figura, temos:

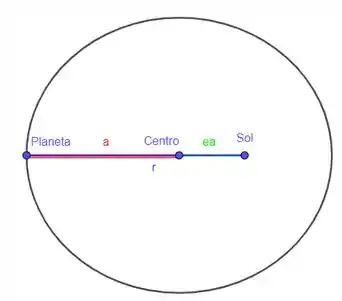
Note que a distância r entre o planeta e o sol, neste outro caso, é dada por:

r = a + e a

r = a ( 1 + e )

Passo 3

(b) Agora, basta substituir os valores de a e e nas expressões do Periélio e do Afélio demonstradas no passo anterior, obtendo assim:

Espero ter ajudado! Abraços e até a próxima!

Resposta

Veja a explicação acima.

Exercícios de Livros Relacionados

Prove que a distância entre os pontos P_1 (r_1 , theta_1) e P_2 ( r_2 , theta_2 ) é sqrt(r_1^2 + r_2^2 - 2 r_1 r_2 c o s ( theta_2 - theta_1 ))
r = 5 3 + 3 s e n θ . (a) ache a excentricidade; (b) identifique a cônica; (c) escreva a equação da diretriz que corresponde ao foco na origem; (d) faça um esboço da curva.
Ache a área da região limitada por um laço da curva r = as e nn θ , onde n é um número inteiro positivo.
Ache a equação polar da circunferência com centro em ( r 0 ,θ 0 ) e raio a unidades.
Ache a equação polar da cônica que satisfaz as condições dadas e faça um esboço do gráfico. A reta rs e n θ = 6 é a diretriz correspondente ao foco na origem e e = 5 3 .