Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.4 - Ex. 8

Movimento de uma partícula No instante t > 0 , a velocidade de um corpo que se desloca ao longo do eixo s é v = t 2 - 4 t + 3 .

  1. Determine a aceleração do corpo cada vez que a velocidade for nula.
  2. Quando o corpo se desloca para a frente? E para trás?
  3. Quando a velocidade do corpo aumenta? E diminui?

Passo 1

Para resolvermos a letra a.) precisamos achar em qual tempo a velocidade é nula,

t 2 - 4 t + 3 = 0

Utilizando Bhaskara:

t = 4 ± - 4 2 - 4 ∙ 1 ∙ 3 2 ∙ 1

t = 4 ± 16 - 12 2

t = 4 ± 4 2

t = 4 ± 2 2

t 1 = 3   s

t 2 = 1   s

Agora, precisamos encontrar a função a t que é a variação da velocidade em relação ao tempo, ou seja, é a derivada de d v t d t .

a t = t 2 - 4 t + 3 '

a t = 2 t 2 - 1 - 4 t 1 - 1 + 0

a t = 2 t - 4

Substituindo os valores de t :

a 1 = 2 ∙ 1 - 4 = - 2   m / s 2

a 3 = 2 ∙ 3 - 4 = 2   m / s 2

Passo 2

Já na letra b.), vamos encontrar quando o corpo se desloca pra frente, ou seja, quando a velocidade é positiva e quando o corpo se desloca pra trás (velocidade negativa). Para isso, vamos fazer um esboço do gráfico para facilitar a visualização:

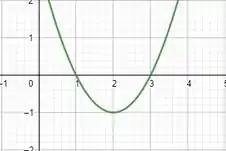
A gente consegue ver no gráfico que no intervalo 1 < t < 3 a velocidade é negativa e quando t < 1 ou t > 3 a velocidade é positiva.

Passo 3

Para resolvermos a letra c.) temos que lembrar que para termos um aumento da velocidade de um corpo, temos que ter uma aceleração positiva e para diminuir, uma aceleração negativa. Vamos fazer de novo um esboço do gráfico.

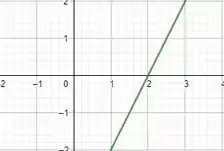
Olhando pro gráfico vemos que para t > 2 a aceleração é positiva e para t < 2 a aceleração é negativa.

Resposta

  1. a 1 = - 2 m / s 2 ;   a 3 = 2   m / s 2
  2. Velocidade positiva: t < 1 ou t > 3 ; Velocidade negativa: 1 < t < 3
  3. Aceleração positiva: t > 2 ; Aceleração negativa: t < 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 33 a 35, use o conceito de taxa relativa, definido como segue se y = f(x), a taxa relativa da variação de y com relação a x em x1 é dada por f ' x 1 f x 1 ou, equivalentemente, dy /
Mostre que para toda função linear f, a taxa média de variação de f(x) quando x varia de x1 até x1+k é a mesma que a taxa de variação instantânea f(x) em x1.
Nos Exercícios de 33 a 35, use o conceito de taxa relativa, definido como segue se y = f(x), a taxa relativa da variação de y com relação a x em x1 é dada por f ' x 1 f x 1 ou, equivalentemente, dy /
Seja x = f t , t ≥ 0 , tal que f 0 = 1 , d x d t0 e d 2 x d t 20 para t ≥ 0 . Como você acha que deve ser o gráfico de f ? Por quê?
Uma partícula desloca-se sobre o eixo x com função de posição x = 1 2 t + 1 , t ≥ 0 .a) Qual a velocidade no instante t ?b) Qual a aceleração no instante t ?c) Esboce o gráfico da função de posição.