Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.2 - Ex. 19
Uma pessoa P, partindo da origem, move-se na direção positiva do eixo x, puxando um peso ao longo da curva C (chamada tratriz), como mostrado na figura 1.24. O peso, inicialmente localizado no eixo em , é puxado por uma corda de comprimento , que é mantida esticada durante todo o movimento. Encontre a equação diferencial da trajetória do movimento. [Sugestão: A corda fica sempre tangente a C, considere o ângulo de inclinação como mostrado na figura.]
Passo 1
Nesse problema, temos um esquema assim:
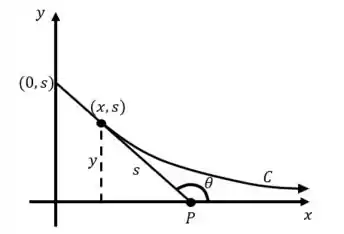
A pessoa saiu da origem e ta carregando um peso que ta ao longo da curva . Ela ta puxando esse peso por uma corda de comprimento que fica sempre esticada. Bom, de uma coisa já sabemos: a corda fica sempre tangente à curva C.
Agora, precisamos encontrar a equação diferencial que define a trajetória do movimento, vamos lá?
Passo 2
Como a reta é sempre tangente à curva , vamos lembrar de derivadas: a inclinação de uma reta tangente a uma curva é a derivada da curva naquele ponto. Dessa forma, temos:
Agora vamos pensar o seguinte:
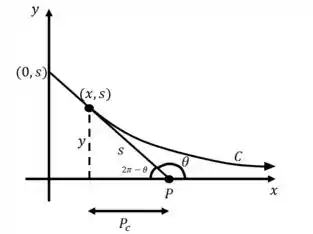
Por trigonometria, temos
Fazendo Pitágoras, temos
Substituindo:
Passo 3
Beleza, chegamos nisso aqui:
Vamos dar uma desenvolvida
De identidades trigonométricas, sabemos que
Então:
Substituindo os valores:
Mas lá no passo 2, vimos que , então:
