Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.9 - Ex. 9
9. Uma pipa está voando a uma altura de 40m. uma criança está empinando-a de tal forma que ela se mova horizontalmente, a uma velocidade de . Se a linha estiver esticada, com qu velocidade a linha estará sendo “dada’’, quando o comprimento da linha desenrolada for de 50 m ?
Passo 1
Vamos seguir os seguintes passos para resolver qualquer questão de taxas:
- Leia cuidadosamente o problema.
- Se possível, faça um diagrama.
- Indentificar as variáveis e as constantes do problema.
- Escreva uma equação que relacione as variáveis.
- Derive em ambos os lados em relação a t usando regra da cadeia.
- Substituir o que foi dado e encontrar o que foi pedido.
Uma ilustração do que a questão está dizendo:
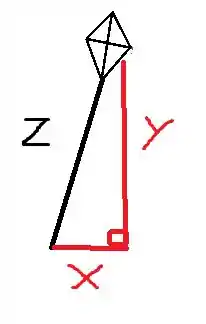
Variaveis:
z – tamanho da linha da pipa é a velocidade com que essa linha é “dada”.
X – distancia horizontal da pipa até o ponto inicial da pipa é a velocidade da pipa.
Constantes:
y- distancia da pipa até o chão
Interpretando os dados que a questão deu:
A questão nos deu a velocidade da pipa:
E quer saber quando o tamanho da linha for 50m.
Passo 2
A equação que descreve o problema é a nossa conhecida fórmula de Pitágoras:
Mas muito cuidado, esse y é constante, então, a derivada de y é zero.
Passo 3
Já ilustramos o que a questão pediu, já encontramos a equação que descreve o problema, agora só falta derivar.
Derivando em ambos os lados em relação a t:
Isolando :
Eitaaaa, já sabemos quem é e z, mas e x??
Teremos que usar Pitágoras novamente para encontrarmos essse danado do x:
Voltando para as nossas derivadas: