Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.4 - Ex. 20
Uma piscina circular tem um diâmetro de pés, os lados têm pés de altura e a profundiade da água é de pés. Quanto trabalho é necessário para bombear toda a água pelo lado da piscina? (Use o fato de que a densidade da água é )
Passo 1
Nós temos um cilindro de de diâmetro, e com uma altura de . Dentro dele, temos água com uma profundidade de .
Então para tirar a primeira “porção” de água, temos que elevá-la por uma altura de . Essa altura vai aumentar conforme tirarmos mais água:
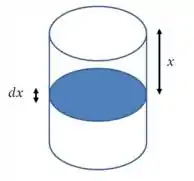
Logo no início, teremos , e quando a água estiver quase acabando, teremos .
Passo 2
Agora vamos calcular o trabalho necessário para elevar um “pequeno cilindro” de altura por uma altura .
O volume desse cilindro é:
E como a densidade da água é , a massa desse volume é:
Passo 3
Então o trabalho necessário para elevar essa massa de água (ignorando a aceleração da gravidade) por pés é:
Agora é só integrar com variando de até :
Resposta
O trabalho necessário é