Enunciado
Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.6 - Ex. 23
Uma piscina retangular tem de largura e de comprimento. A tabela a seguir mostra a profundidade h(x) da água em intervalos de de uma extremidade da piscina até a outra. Estime o volume de água da piscina usando a regra do trapézio com aplicada à integral
Passo 1
Esse questão é ótima para treinarmos mais uma técnica de integração. A regra do Trapézio. Ela pode vir a ser útil para safar a sua vida durante uma prova. Então vamos lá.
O primeiro comentário que eu tenho a fazer é : Se você tentar dar uma de esperto, pode dar um mole que vai te custar uns pontos.
Por exemplo, temos a tabela com os valores e alturas e você percebe que poderia fazer a regra do trapézio, com o trapézio enorme que é a piscina ao invés de vários trapézios pequenos. Você pode pensar que a piscina é assim :
E que logo a conta seria
E pronto problema resolvido. Mas tenho que te informar. Isso não está certo.
Plotando os valores numa tabela vemos que esse fundo da piscina é mais desse tipo
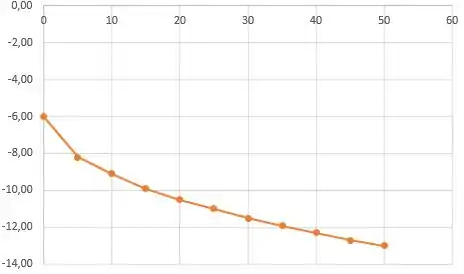
Logo nos dois primeiros pontos de descida vemos que está muito diferente do que idealizamos. Logo nosso volume também será bem diferente.
Passo 2
MAS okay, já que pelo método mais rápido não funciona. Vamos treinar o método proposto pelo enunciado
Se formos pegar pequenos trapézios podemos falar que a área deles é
Está vendo que podemos agrupar essa soma? Então vamos arrumar isso!
E pronto essa é a forma geral do método dos trapézios, vamos jogar os nossos valores dentro, lembrando que nosso
Nossos pontos deram erro logo no inicio e puderam mostrar para a gente que a curvatura era disforme. Mas do mesmo jeito que foi no início, numa outra questão poderia ser no meio, no final, ou tudo disforme. Então utilizar esse novo truque pode te gerar uns pontos a mais na prova.
Por aqui terminamos, te encontro na próxima resolução. : )