Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 28

Uma piscina tem 5   m de largura por 10   m de comprimento, 1   m de profundidade na parte rasa e 3   m na parte mais funda. Sua secção transversal está mostrada na figura. Se a piscina for enchida a uma taxa de 0,1   m 3 / m i n , quão rápido estará subindo o nível da água no ponto mais profundo for de 1   m ?

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente determinar o quão rápido estará subindo nível da água da piscina no ponto mais profundo de 1   m . Isso quer dizer que nós precisamos encontrar a taxa de variação da altura da água dessa piscina h ' ( t ) .

Só que para encontrar essa altura, precisamos antes determinar a taxa de variação do volume de água da piscina. Dessa forma, vamos aproximar o formato da piscina por um trapézio, de forma que a gente consiga encontrar a relação entre o volume V e a altura h da água.

Em seguida, vamos derivar essas relações e substituir o ponto que o enunciado nos deu para encontramos nossa resposta.

Vamos lá!

Passo 2

Se esboçamos o trapézio da secção transversal da piscina como:

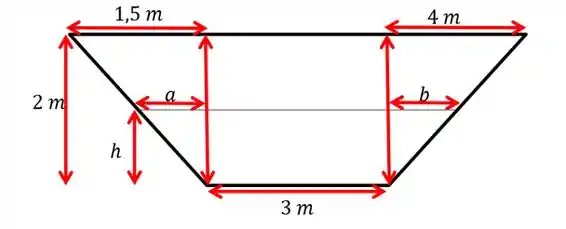
Então, até que a altura h seja 2 metros, o volume da água é dado por:

V = 5 ∙ a h 2 + 3 h + b h 2

Para achar a relação entre a altura e os valore de a e b pode ser obtida por semelhança de triângulos:

a 1,5 = h 2 ⇒ a = 1,5 h 2

b 4 = h 2   ⇒ b = 2 h

Logo, o volume é dado por:

V = 5 ∙ 1,5 h 2 h 2 + 3 h + ( 2 h ) h 2

V = 5 ∙ 1,5 h 2 4 + 3 h + h 2

V = 5 ∙ 3 h + 11 8 h 2

Passo 3

Então, derivando V em função do tempo t implicitamente, temos:

V ' t = 5 ∙ 3 h ' t + 11 4 h ∙ h ' t

V ' t = 5 h ' t ∙ 3 + 11 4 h

E isolando h ' ( t ) , obtemos:

h ' t = V ' t 5 3 + 11 4 h

Passo 4

Então, quando o ponto mais profundo for h = 1   m e V ' t = 0,1   m 3 / m i n , teremos:

h ' t = 0,1 5 3 + 11 4 1

h ' t = 2 575

Logo, o nível da água estará subindo a uma taxa de 2 575 m/min.

Valeu, galera! Até a próxima! 😉

Resposta

2 575   m / m i n

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A quantia em dinheiro no custo total da produção de x unidades de certa mercadoria é dada por C x = 40 + 3 x + 9 2 x . Ache (a) o custo marginal quando 50 unidades são produzidas e (b) o número de uni
Uma imobiliária que administra um condomínio aluga cada apartamento por $ p por mês quando x apartamentos são alugados por p = 30 300 - 2 x . Se $ R ( x ) for o rendimento recebido do aluguel de x apa
Um helicóptero deixa o solo num ponto a 250 m de um observador e sobe verticalmente a 7,5 m/s. Ache a taxa de variação no tempo da medida do ângulo de elevação do helicóptero quando ele estiver a 180
Um quadro com 150 cm é colocado numa parede com sua base a 210 cm do nível dos olhos de um observador. Se o observador está se aproximando da parede com uma velocidade de 90 cm/s, com que velocidade a
Um avião está voando a uma velocidade de 300 km/h, a uma altitude de 4 km. Se um observador está no chão, ache a taxa de variação no tempo da medida do ângulo de elevação do avião em relação ao observ