Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 27

Um cocho de água tem 10   m de comprimento e uma secção transversal com a forma de um trapezoide isósceles com 30   c m de comprimento na base, 80   c m de extensão no topo e   50   c m de altura. Se o cocho for preenchido com agua a uma taxa de 0,2   m 3 / m i n , quão rápido estará subindo o nível da água quando ela tiver 30   c m de profundidade?

Passo 1

Opa, bora lá! Essa questão fala de um cocho enchendo de água. Se você não sabe o que é um cocho ele é um recipiente que é usando pra vacas e bois se alimentarem ou beberem água. O nosso tem a forma de um prisma reto de base trapezoide, só que com a menor face virada para baixo. A seguir, um desenho para ilustrar:

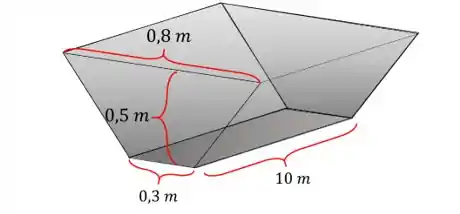
Temos uma vazão de água enchendo o coho de 0,2   m 3 / m i n queremos:

h ' t = ? ? ?

Quando a produndidade da água for h = 30   c m .

Passo 2

Assim, para cada nível de água, temos uma altura h , para a qual o volume da água é:

V =     10 × 1 2 × 0,3 + 0,3 + 2 a × h

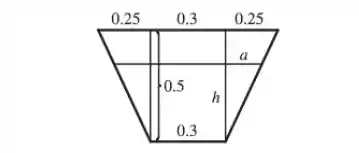
Por semelhança de triângulos, a se relacina com h da seguinte forma:

a h = 0,25 0,5

a = h 2

Então, o volume é:

V = 5 0,6 + h × h

V = 3 h + 5 h 2

Passo 3

Então, derivando as funções em relação ao tempo t em minutos, temos:

V ' t = 3 h ' t + 10 h × h ' ( t )

V ' t = ( 3 + 10 h ) × h ' ( t )

h ' t = V ' t 3 + 10 h

Já que quando h = 0,3 m e V ' t = 0,2   m 3 / m i n então:

h ' t = 0,2 3 + 10 ( 0,3 )

h ' t = 1 30

Logo, a altura está variando a uma taxa de 1 30 m/min.

Resposta

A altura está variando a uma taxa de 1 30 m/min.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

23. A lei de Boyle para a expansão de um gás é P V = C , onde P é a pressão em quilogramas força por unidade de área, V é o número de unidades de volume do gás e C é uma constante. Mostre que V decres
21. Se A xc m 2 for a área de um quadrado e s cm for o comprimento de cada lado, ache a taxa de variação de A x em relação a x, quando x varia de (a) 4,000 a 4,600; (b) 4,000 a 4,300; (c) 4,000 a 4,10
Um objeto move-se ao longo de uma reta, de acordo com a equação de movimento s = 5 + t 2 , com t ≥ 0 . Ache o valor de t para o qual a medida da velocidade instantânea é (a) 0 ; (b) 1 .
Um objeto move-se ao longo de uma reta, de acordo com a equação de movimento s = 4 t 2 + 3 , com t ≥ 0 . Ache o valor de t para o qual a medida da velocidade instantânea é (a) 0 ; (b) 1 ; (c) 2 .
Suponha que um líquido seja produzido por um certo processo químico e que a função custo total C seja dada por C x = 6 + 4 x , onde C ( x ) é a quantia correspondente ao custo total da produção de x l