Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.6 - Ex. 18
18- Plote a parábola e sua diretriz. Também plote a curva obtida pela rotação dessa parábola ao redor de seu foco por um ângulo .
Passo 1
Eaee, tudo certinho?? Bom... queremos plotar a parábola dada pela seguinte equação polar:
Também queremos plotar a diretriz .
Para isso, vamos comparar a nossa equação com a seguinte equação geral:
Onde é a diretriz e é a excentricidade.
Em seguida, queremos plotar também a curva obtida pela rotação dessa parábola ao redor de seu foco por um ângulo .
Passo 2
Antes de plotar o gráfico vamos encontrar a equação da diretriz ao multiplicar o numerador e o denominador dessa parábola por :
Como a excentricidade vale e o denominador tem um seno positivo então a equação da diretriz vale:
Onde é encontrado por:
Logo:
Passo 3
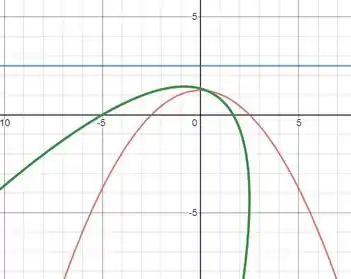
Pela equação que nos foi dada, teremos uma parábola com concavidade voltada para baixo.
O foco será o ponto . Lembrando que a diretriz é .
Assim, plotando o nosso gráfico, temos:
Onde a reta em azul é a diretriz.
Passo 4
Agora a rotação dessa parábola entorno de seu centro em um ângulo de (no sentido horário ) e no sentido anti-horário será igual a:
Plotando o gráfico girado no sentido horário nós teremos a curva verde:
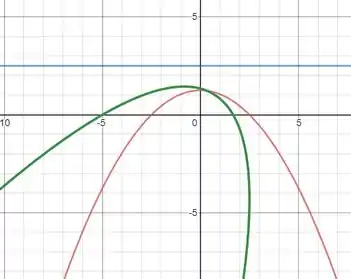
Resposta
