Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.6 - Ex. 16
16- a) Encontre a excentricidade, b) identifique a cônica, c) dê uma equação da diretriz e d) esboce a cônica.
Passo 1
Fala ai! Vamos lembrar de um teorema importante citado no livro que vai nos ajudar a resolver essa questãozinha.
a) Teorema 6:
Equação polar tem a forma.
Lembrando que é a excentricidade.
Note que o denominador está como então temos que transformar esse denominador de modo que temos a soma de 1 com algum fator trigonométrico.
Dividindo o numerador e o denominador por nós teremos uma equação normalizada de acordo com o teorema . Com isso nós teremos:
Temos a excentricidade.
E como a excentricidade é menor do que , logo a cônica será uma elipse.
Passo 2
b) Vamos lembrar que:
- Se A elipse é uma elipse de formato alongado, onde 𝑒e representa o quão longe os focos estão do centro em relação ao tamanho da elipse.
- Se : A elipse é na verdade um círculo (caso especial de elipse com excentricidade zero).
- Se : A elipse é uma parábola (caso especial de elipse onde os focos estão infinitamente distantes).
Sendo assim, como , ou seja, menor que 1, a equação representa uma elipse.
Passo 3
Pelo denominador estar com uma função seno então sabemos que a diretriz é uma reta e por ser positiva sabemos que ela é um valor de positivo, logo a equação da reta diretriz vale:
Passo 4
Os vértices dessa cônica estarão em e pois são os valores máximos e mínimos de cosseno, o que nos dá os pontos polares:
Fazendo o ponto médio nós encontraremos o seguinte ponto médio:
Passo 5
Colocando em um software os pontos encontrados no Passo 2, obtermos o seguinte gráfico da função:
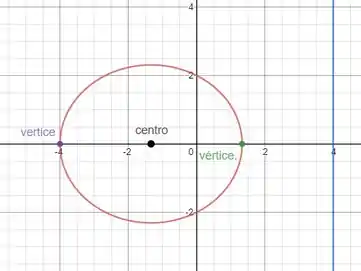
Parâmetros:
