Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.Exercícios Práticos - Ex. 33

f ( x ) =   x ( x 2 -   1 ) x 2 -   1       pode ser estendido em x   =   1 ou x   = - 1 ? Justifique suas respostas. (Faça o gráfico da função; ele será interessante.)

Passo 1

Para descobrirmos sobre a possibilidade de uma extensão contínua, precisamos analisar a existência dos limites da função para x   =   1 e para x   = - 1 .

Passo 2

Para um limite existir em x   =   1 , é necessário que lim x → 1 + ⁡ f ( x )   =   l i m x → 1 -   f ( x )  

Calculando o limite para x → 1 +

x 2 -   1   =   x 2 -   1  

Pois, quando   x → 1 + ,       x 2 >   1

Logo,

l i m   x → 1 +   x ( x 2 -   1 ) x 2 -   1   =   l i m   x → 1 +   x ( x 2 -   1 ) x 2 -   1    

l i m   x → 1 +   x   =   1

Calculando o limite para x → 1 -

x 2 -   1   = - ( x 2 -   1 )  

Pois, quando x → 1 - ,       x 2 <   1

Logo,

l i m x → 1 -   x ( x 2 -   1 ) x 2 -   1   =   l i m x → 1 -   x ( x 2 -   1 ) - ( x 2 -   1 )

l i m x → 1 -   - x   =   - 1

Logo, lim x → 1 + ⁡ f ( x )   ≠   l i m x → 1 -   f ( x )  

Passo 3

Para um limite existir em x = -1, é necessário que lim x → - 1 + ⁡ f ( x )   =   l i m x → - 1 -   f ( x )  

Calculando o limite para x → - 1 +

x 2 -   1   =   - ( x 2 -   1 )  

l i m   x → - 1 +   x ( x 2 -   1 ) x 2 -   1   =   l i m   x → - 1 +   x ( x 2 -   1 ) - ( x 2 -   1 )    

l i m   x → - 1 +   - x   =   1

Calculando o limite para x → 1 -

x 2 -   1   = x 2 -   1  

l i m x → - 1 -   x ( x 2 -   1 ) x 2 -   1   =   l i m x → - 1 -   x ( x 2 -   1 ) x 2 -   1

l i m x → - 1 -   x   =   - 1

Logo, lim x → - 1 + ⁡ f ( x )   ≠   l i m x → - 1 -   f ( x )  

Passo 4

Visualizando o gráfico, é possível notar que não existe limite em x = 1 e em x = -1

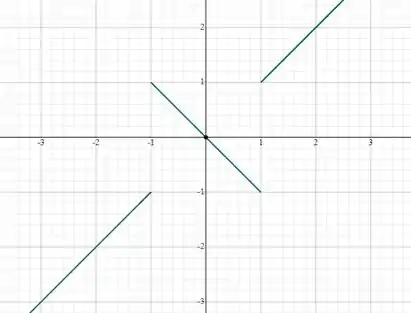
Resposta

A função f(x) não pode ser estendida em x=1 ou em x=-1, pois não há limite da função para esses pontos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 49-52, represente graficamente a função f para verificar se ela parece ter uma extensão contínua na origem. Em caso afirmativo, utilize os comandos "Trace" e "Zoom" para determinar um b
Nos Exercícios 35-38, faça o gráfico da função indicada para verificar se ele parece ter uma extensão contínua no ponto a dado. Em caso afirmativo, utilize as ferramentas "Trace" e "Zoom" para determi
Nos Exercícios 35-38, faça o gráfico da função indicada para verificar se ele parece ter uma extensão contínua no ponto a dado. Em caso afirmativo, utilize as ferramentas "Trace" e "Zoom" para determi
Nos Exercícios 35-38, faça o gráfico da função indicada para verificar se ele parece ter uma extensão contínua no ponto a dado. Em caso afirmativo, utilize as ferramentas "Trace" e "Zoom" para determi
Nos Exercícios 35-38, faça o gráfico da função indicada para verificar se ele parece ter uma extensão contínua no ponto a dado. Em caso afirmativo, utilize as ferramentas "Trace" e "Zoom" para determi