Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.Exercícios Práticos - Ex. 36
Nos Exercícios 35-38, faça o gráfico da função indicada para verificar se ele parece ter uma extensão contínua no ponto a dado. Em caso afirmativo, utilize as ferramentas "Trace" e "Zoom" para determinar um bom candidato para o valor da função estendida em a. Se a função não aparentar ter uma extensão contínua, ela poderá ser estendida para ser contínua à direita ou à esquerda? Em caso afirmativo, qual você acha que deve ser o valor da função estendida?
36.
Passo 1
a.
A gente precisa de algum software para desenhar esse gráfico, eu vou usar o GeoGebra, mas da para fazer com qualquer um.
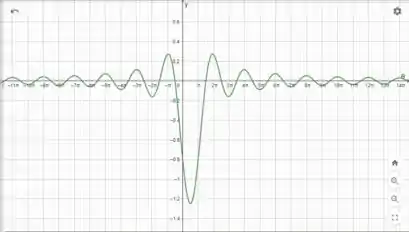
Escrevendo a função nele vamos ter esse gráfico:
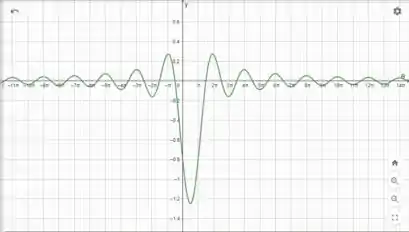
Podemos ver que a função parece ser continua em
Passo 2
Para descobrirmos o candidato ao valor da função extendida vamos dar um zoom bem grande na função em :
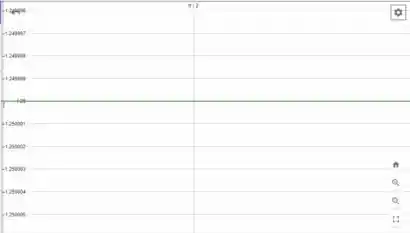
Podemos observar que o melhor candidato para a função extendida no ponto é
Resposta
