Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.1 - Ex. 56
Em qual ponto sobre a curva a reta tangente é paralela à reta ? Ilustre fazendo o gráfico da curva e de ambas as retas.
Passo 1
E aí! Tudo certinho?
Nesse problema queremos saber em que ponto da curva está a reta tangente paralela à reta .
Então, essa reta tangente deverá possuir o mesmo coeficiente angular .
Pela reta dada, tiramos que . Sabemos também que
Veja só!
Passo 2
Então, teremos a seguinte equação para resolver em :
Logo, pela equação da curva temos que:
Portanto, o ponto será .
Sacou?
Passo 3
Gráfico:
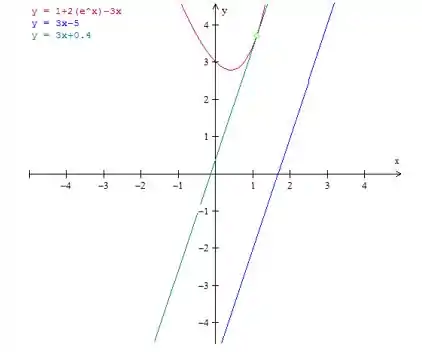
E aí! Entendeu tudo? Responde Aí!
Resposta
Exercícios de Livros Relacionados
Determine os pontos na curva y = 2 x 3 - 3 x 2 - 12 x + 20 em que a tangente seja a. perpendicular à reta y = 1 - x 24 .b. paralela à reta y = 2 - 1 2 x .
A parábola y = x 2 + C deve ser tangente à reta y = x . Encontre C .
Mostre que a tangente à curva y = x 3 em qualquer ponto ( a ,a 3 ) intercepta a curva novamente em um ponto em que o coeficiente angular é quatro vezes o coeficiente angular em ( a ,a 3 ) .
Há algum ponto na curva y =x - e - x em que o coeficiente angular seja 2? Se houver, encontre-o.
Para qual valor de c a curva y = c / ( x + 1 ) é tangente à reta que passa pelos pontos ( 0 ,3 ) e ( 5 , - 2 ) ?