A posição de uma partícula que se desloca ao longo de eixo varia com o tempo segundo a equação , , em que e são constantes estritamente positivas.

a) Qual a velocidade no instante ?

b) Com argumentos físicos, justifique a afirmação: “a função é estritamente crescente”.

c) Qual a aceleração no instante ?

d) Com argumentos físicos, justifique a afirmação: “o gráfico da função tem a concavidade voltada para baixo”.

e) Calcule .

f) Esboce o gráfico da função.

b) Se é uma constante estritamente positiva, e como um número positivo, não nulo, elevado a qualquer coisa sempre será positivo, mas também nunca será zero, então temos que .

Assim, a velocidade sempre será positiva, e se isso acontecer, em todo instante, teremos valores de maiores que os valores dos instantes anteriores. Logo, podemos concluir que a função é estritamente crescente.

c) A aceleração é a derivada da velocidade, então:

d) Como os termos , e são todos positivos, temos que é sempre negativo, ou seja, temos sempre uma aceleração negativa que faz com que a velocidade diminua.

Se a velocidade está sempre diminuindo, mas é sempre positiva, à medida que aumentamos , o valor de cresce cada vez mais lentamente. Esse movimento descreve uma curva cuja concavidade é voltada para baixo. Logo, podemos concluir que o gráfico da função tem a concavidade voltada para baixo.

e) Para temos:

Então:

f) Assim, podemos esboçar o gráfico da função como:

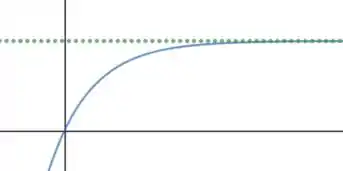
Onde a reta pontilhada em verde é a reta em que a função se alinha quando tende ao infinito.