Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.15 - Ex. 21
Dois pontos e deslocam-se, respectivamente, nos eixos e de modo que a soma das distâncias de a e de a mantém-se constante e igual a durante o movimento, em que é um ponto fixo. (Veja a figura a seguir.)
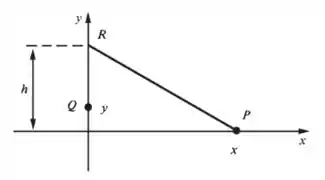
Relacione a velocidade de com a velocidade de .
Passo 1
Temos que:
A distância de a é dada por:
A distância de a é dada por:
Passo 2
Então, se sua soma é constante e igual a :
Agora precisamos derivar em relação a :
Logo, a relação entre a velocidade de e a velocidade de é dada por .
Resposta
A relação entre a velocidade de e a velocidade de é dada por .
Exercícios de Livros Relacionados
Seja f t = t 3 + 3 t 2 .a) Estude o sinal de f ' t .b) Estude o sinal de f ' ' t .c) Calcule lim t → + ∞ t 3 + 3 t 2 e lim t → - ∞ t 3 + 3 t 2 .d) Utilizando as informações acima, esboce o gráfico
A equação abaixo da a posição s = f ( t ) de um corpo que se desloca em uma reta coordenada (s em metros, t em segundos). Determine a velocidade, o módulo da velocidade, a aceleração e a sobreaceleraç
A equação abaixo da a posição s = f ( t ) de um corpo que se desloca em uma reta coordenada (s em metros, t em segundos). Determine a velocidade, o módulo da velocidade, a aceleração e a sobreaceleraç
23. A lei de Boyle para a expansão de um gás é P V = C , onde P é a pressão em quilogramas força por unidade de área, V é o número de unidades de volume do gás e C é uma constante. Mostre que V decres
21. Se A xc m 2 for a área de um quadrado e s cm for o comprimento de cada lado, ache a taxa de variação de A x em relação a x, quando x varia de (a) 4,000 a 4,600; (b) 4,000 a 4,300; (c) 4,000 a 4,10