Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.7 - Ex. 30
Um pôster deve ter uma área de 180 pol² com uma borda de 1 polegada na base e nos lados, e uma borda de 2 polegadas em cima. Que dimensões darão a maior área impressa?
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver esse problema de otimização.
Em problemas de otimização como esse, devemos tentar representar a quantidade que queremos minimizar ou maximizar em função de um só parâmetro (nesse caso, largura do pôster), para então analisar essa função e encontrar os extremos. A imagem mostra o pôster:
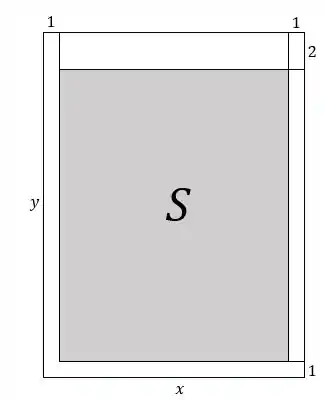
Vamos então tentar representar a área de impressão , em cinza na figura, em função de .
Passo 2
Primeiro vamos eliminar a variável , que é a altura do pôster. Como a área é fixa em 180 pol², temos:
Sendo e representados em polegadas. Agora vamos representar a área . Ela tem altura
e largura
então a área é:
Colocamos agora apenas em função de :
Passo 3
Agora temos a área de impressão em função de , e devemos encontrar o máximo dessa função.
Como é uma distância, deve ser um número positivo, então vamos investigar a função para no intervalo .
Podemos ter um ponto crítico se a derivada da função for zero ou não existir. Vamos derivar
Como essa função sempre existe para , vamos investigar . Temos:
Repare que foi descartado pois deve ser positivo. Agora devemos verificar se em temos um valor máximo. Se , podemos ver que é positivo, então a função é crescente. Se , é negativo e então a função é decrescente.
Como a função é crescente antes e decrescente depois de , temos aí um ponto máximo.
Passo 4
Sabemos que é um ponto máximo, mas agora devemos saber se é o máximo absoluto.
Como esse é o único ponto crítico, agora basta olhar a função nos extremos do intervalo. Devemos então olhar os casos em que e que :
Como a função vai a menos infinito nos extremos do intervalo e é o único ponto máximo local, é o ponto máximo absoluto. Vamos então calcular também o valor de :
Resposta
Altura de polegadas, largura de polegadas