Uma prancha de está apoiada em uma parede. Se em um certo instante sua base está a da parede e sendo empurrada em direção a esta a uma taxa de , com que rapidez estará crescendo o ângulo agudo que a prancha faz com o solo?
Passo 1
Vamos analisar com calma o que está acontecendo:
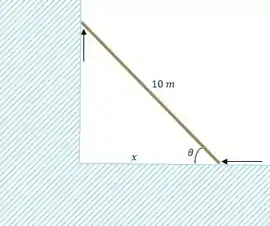
A base da prancha irá se aproximar da parede, de forma que o seu topo deslize para cima e além disso o ângulo agudo que a prancha faz com o solo (que chamamos de ) aumente, concorda?
Pra relacionar esses caras temos que usar algo que envolva ângulo de triângulos retângulos e alguns de seus lados. No nosso caso o lado adjacente ao ângulo e a hipotenusa. Opa então vamos falar que:
Passo 2
Pra relacionarmos as taxas com que e variam quando a prancha se move, podemos derivar essa expressão em relação ao tempo, fica assim ó:
Usando a regra da cadeira vamos chegar que:
Porém a derivada de cosseno é menos o seno, lembra? Então chegamos na seguinte relação:
Passo 3
Para gente descobrir a rapidez que estará crescendo o ângulo agudo () que a prancha faz com o solo, basta descobrirmos o naquele instante, concorda? Mas o que significam aqueles outros dados que o enunciado nos dá?
A base sendo empurrada em direção a parede a uma taxa de nos diz que:
Lembrando de atentar pro sinal negativo, pois se a base está se aproximando, está diminuindo.
Só que pra usarmos a expressão que encontramos ali em cima ainda precisaríamos descobrir o nesse instante. Pra isso podemos usar que:
E ainda pela Relação Fundamental Trigonométrica:
Passo 4
Showww, aí so precisamos substituir todos esses dados na expressão que encontramos ali em cima, ficamos com:
Então como tínhamos combinado, a rapidez que estará crescendo o ângulo agudo () que a prancha faz com o solo é justamente o . Então encontramos nossa resposta 😊
PS: Perceba que encontramos um , o que faz bastante sentido, porque está aumentando.