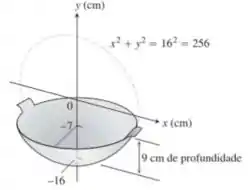
Projeto de uma frigideira. Você está projetando uma frigideira que terá o formato de uma tigela esférica com alças. Ao fazer uma experimentação em casa, percebe que conseguirá um modelo com cerca de de capacidade, se a profundidade for de e o raio da esfera, . Para ter certeza, você desenha a frigideira como um sólido de revolução, como se vê na figura, e calcula seu volume com uma integral. Arredondando para o inteiro mais próximo, qual será o volume obtido em ? .

Então pessoal, por mais que pelo desenho a questão aparente ser complicada, isso é só impressão! Essa questão se trata de um cálculo comum de volume de um sólido de revolução! Como a profunidade da frigideira foi dada na vertical, isto é, no eixo , então temos que encontrar uma expressão em função de , obrigatoriamente! Segundo o George, para calcularmos o volume de um sólido em função do eixo , basta calcularmos a seguinte integral:

Os intervalos de integração a figura nos dá, não é mesmo? Pela imagem e (do mais negativo para o menos negativo). Mas po, quem é esse aí, senhor amado?

Esse termo aí é a função raio do sólido que, segundo a figura, é dado pela equação:

Como queremos uma expressão de , então: