Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 76
a. Prove que é crescente para x > 1.
b. Usando o item (a), mostre que .
Passo 1
Item a :
Vamos derivar a função:
Temos que x= 1 é um ponto crítico do gráfico, pois:
Sabemos que a função é crescente nos pontos onde a derivada é positiva, então vejamos:
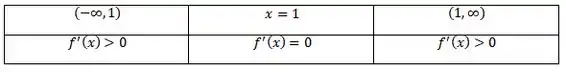
(Veja que 1 é sempre maior que uma fração com numerador 1)
Portanto, a função é crescente para x > 1 .
Passo 2
Item b:
Temos pelo item anterior que a função é sempre crescente para x >1. Veja também que:
Bom, se a função em x = 1 é positiva e com x >1 é crescente, concluímos que a função é sempre positiva para x > 1. Então...
E daí...
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
(Teorema de Darboux.) Suponha g derivável em [ a , b ] . Com g ' a0 e g ' b0 . Prove que existe c em ] a , b [ tal que g ’ ( c ) = 0
(Teorema de Darboux.) Suponha g derivável em [a,b]. Com g ' a0 e g ' b0 . Prove que existe c em ]a,b[ talque g ’ ( c ) = 0
Seja y = f ( x ) derivável até a segunda ordem em ] - r , r [ ,r0 , tal que, para todo x ∈ ] - r , r [ , : f ' x - f x - x f x 2 = 0 Prove que f não admite ponto de máximo local em ] 0 , r ] . Prove q
Suponha que f admite derivada de 3º ordem contínua no intervalo aberto I e seja p ∈I . Prove que se f ' p = f ' ' p = f ' ' ' p = 0 e f 4 p ≠ 0 , então p será ponto de máximo local se f 4 p0 e será po
Suponha que f admite derivada de 3º ordem contínua no intervalo aberto I e seja p ∈I . Prove que se f ' p = f ' ' p = 0 e f ' ' ' p ≠ 0 então p é um ponto de inflexão horizontal.