Prove, pela definição, que a função dada é contínua no ponto dado.
em
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente provar que a função é contínua no ponto , usando a definição de continuidade.
Para provar que é contínua em temos que mostrar que para um existe um intervalo aberto que contenha , de modo que:
Isso significa que se pegarmos um qualquer que pertença a um intervalo que é a “vizinhança” de , o valor da função nesse (isto é, ) deve estar no máximo a um de distância de .
Agora vamos aplicar!
Passo 2
Como temos que,
Substituindo na inequação, vamos ter:
Supondo contínua em , temos , ou seja:
Tirando a raiz cúbica de todos os termos, temos:
Agora temos que definir o intervalo
Passo 3
Assim, podemos definir o nosso intervalo como sendo:
De modo que . Ou seja, qualquer que tomemos nesse intervalo obrigatoriamente implicará em:
Como pertence ao intervalo , provamos que a função é contínua. Da até pra ver isso num gráfico, saca só:
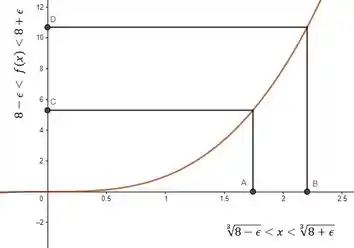
No gráfico-exemplo, temos . Logo, está provado que é contínua em !
Valeu, galera! Até a próxima! 😉