Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.5 - Ex. 54
- Prove que a equação tem pelo menos uma raiz real. (b) Use recursos gráficos para encontrar a raiz correta até a terceira casa decimal
54.
Passo 1
Olá, meu nobre. Pronto para aprender hoje?
Aqui temos uma questão que muitos alunos não gostam, pois devemos provar algo. Mas veja bem, vai ser mais fácil do que parece.
A ideia aqui é utilizar o Teorema de Valor Intermediária para descobrirmos um valor de positivo e outro negativo, pois de acordo com o Teorema, podemos afirmar que existe uma raiz entre esses valores de (um positivo e outro negativo).
O teorema do valor intermediário diz o seguinte:
Suponha que f seja contínua em um intervalo fechado e seja um número qualquer entre e , em que . Existe um número em tal que .
Resumindo, a gente precisa escolher um intervalo , onde o nosso número , que no nosso caso é zero está entre:
Passo 2
Vamos primeiro reescrever nossa equação:
Agora colocando em função de
é um polinômio, e por ser um polinômio é continua em todo o seu domínio, que nesse caso é:
Nosso objetivo então é descobrir dois valores de tais que o esteja entre eles:
Para encontrarmos quais são esses valores cabe uma análise da função.
Jogaremos valores aleatórios para , até encontrarmos dois valores nos quais o esteja entre eles:
Opa! Entre e a função muda de sinal, logo tem pelo menos uma raiz nesse intervalo.
Passo 3
Quando e , temos dois valores em que o está contido entre eles, como é contínua, podemos afirmar que existe um valor para o qual , e esse valor está entre :
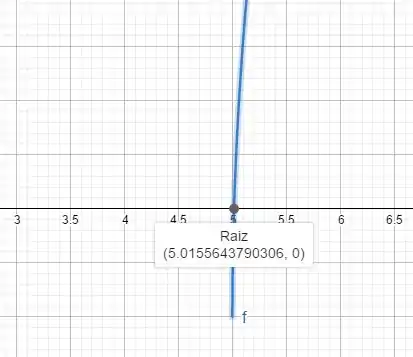
Raiz, pelo método gráfico é
Resposta
Raiz, pelo método gráfico é