Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.7 - Ex. 49
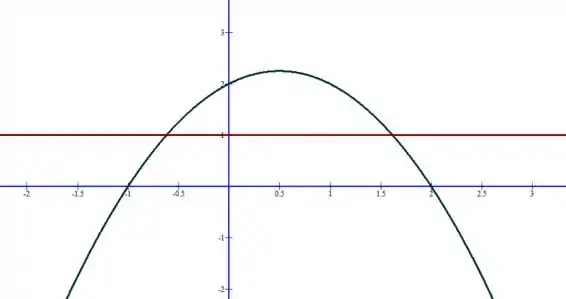
Determine se o teorema do valor intermediário se aplica para ,
Caso seja aplicável, encontre C tal que . Se não for, explique o por que. Faça um esboço da curva e da reta
Passo 1
Como nossa função é polinomial, então é contínua e podemos aplicar tranquilamente o teorema do valor intermediário. Vamos testar então para os extremos do intervalo:
Assim, como , podemos aplicar o TVI.
Ou seja, existe um tal que .
Passo 2
Como mostramos que é aplicável, vamos calcular esse valor de C. Temos:
Resolvendo, encontraremos e .
Como o segundo valor de x é negativo, nosso único candidato a C é .
Logo,
Passo 3
Fazendo um esboço, temos:
Resposta
Exercícios de Livros Relacionados
( a ) Demonstre que a equação tem pelo menos uma raiz real. ( b ) Use sua calculadora para encontrar um intervalo de comprimento 0,01 que contenha a raiz. f x = x 5 - x 2 + 2 x + 3 = 0
( a ) Demonstre que a equação tem pelo menos uma raiz real. ( b ) Use sua ferramenta gráfica para encontrar a raiz correta até a terceira casa decimal. f x = a r c t gx = 1 - x
Existe um número que é exatamente um a mais que seu cubo?
( a ) Demonstre que a equação tem pelo menos uma raiz real. ( b ) Use sua ferramenta gráfica para encontrar a raiz correta até a terceira casa decimal. f x = 100 e - x 100 = 0 . 01 x 2
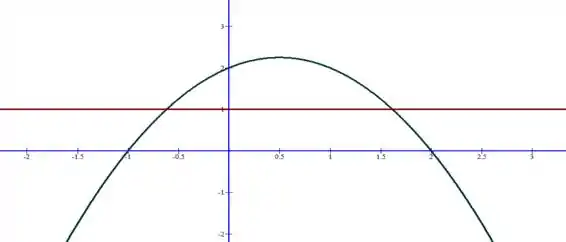
Um monge tibetano deixa o monastério às 7 horas da manhã e segue sua caminhada usual para o topo da montanha, chegado lá as 7 horas da noite. Na manhã seguinte, ele parte do topo às 7 horas da manhã,