Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.3 - Ex. 41
Prove que se for um ponto cujas coordenadas satisfazem a equação , então:
onde e são os focos da hipérbole da Figura 2. (Sugestão: use o método similar sugerido para a elipse nos Exercícios 42 e 43 dos exercícios 10.2.)
Passo 1
As informações que temos, segundo a teoria do livro, são essas:
No qual a primeira equação é a equação da hipérbole e a segunda fórmula se refere ao ponto dos focos da hipérbole. Antes de iniciar os cálculos, vamos plotar novamente a hipérbole da figura 2, saca só:
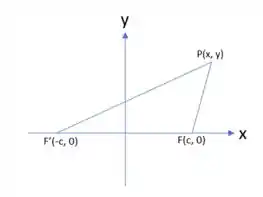
Passo 2
Da figura acima, nós temos o seguinte, galera:
Então, para facilitar, vamos resolver só dentro da raíz, ok? Além disso, como o que muda é apenas o sinal de , então vamos resolver apenas uma expressão do teorema com , belê? Tá confuso? Prometo que não é um bixo de 7 cabeças, saca só:
Mas quem é ? Da expressão
Temos que:
Substituindo, teremos:
Ademais, temos que , onde:
Passo 3
Agora que temos simplificamos as expressão que se encontravam dentro das raízes, de acordo com enunciado, temos:
C.Q.D.
Resposta
Ei, a resposta está no passo a passo :)