Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 46

Se f x = x + 1 x 2 + 1 , prove que o gráfico de f tem três pontos de inflexão que são colineares. Faça um esboço do gráfico.

Passo 1

Para analisar os pontos de inflexão, devemos olhar a segunda derivada. Vamos derivar f utilizando a regra do quociente.

f ' x = 1 x 2 + 1 - ( x + 1 ) ( 2 x ) x 2 + 1 2 = x 2 + 1 - 2 x 2 - 2 x x 2 + 1 2 = - x 2 - 2 x + 1 x 2 + 1 2

f ' ' x = - 2 x - 2 x 2 + 1 2 - ( - x 2 - 2 x + 1 ) 2 ( x 2 + 1 ) 2 ( 2 x ) x 2 + 1 4

f ' ' x = 2 - x - 1 x 2 + 1 - - x 2 - 2 x + 1 2 x x 2 + 1 3

f ' ' ( x ) = 2 [ - x 3 - x - x 2 - 1 + 2 x 3 + 4 x 2 - 2 x ] x 2 + 1 3 = 2 [ x 3 + 3 x 2 - 3 x - 1 ] x 2 + 1 3

f ' ' x = 2 ( x 2 + 4 x + 1 ) ( x - 1 ) x 2 + 1 3 = 2 x - 3 - 2 x - - 2 - 3 ( x - 1 ) x 2 + 1 3

Perceba que x 1 = 3 - 2 , x 2 = - 2 - 3 e x 3 = 1 são raízes de f ' ' ( x ) . Dessa forma, vemos que temos três pontos de inflexão.

Passo 2

Para verificar que os pontos são colineares, vamos fazer f ( x 1 ) , f x 2 ,   f ( x 3 ) e calcular o coeficiente angular.

f x 1 = f 3 - 2 = 3 - 2 + 1 3 - 2 2 + 1 = 3 - 1 3 - 4 3 + 4 + 1 = 3 - 1 8 - 4 3 = 3 - 1 4 2 - 3 =

f x 1 = ( 3 - 1 ) ( 2 + 3 ) 4 4 - 3 = 2 3 - 2 + 3 - 3 4 = 3 + 1 4

f x 2 = f - 2 - 3 = - 2 - 3 + 1 - 2 - 3 2 + 1 = - 1 - 3 2 + 3 2 + 1 = - 1 - 3 4 + 4 3 + 3 + 1 = - 1 - 3 8 + 4 3

f x 2 = - 1 - 3 4 2 + 3 = ( - 1 - 3 ) ( 2 - 3 ) 4 4 - 3 = - 2 - 2 3 + 3 + 3 4 = 1 - 3 4

f x 3 = f 1 = 1 + 1 1 2 + 1 = 1

Agora calculamos o coeficiente angular da reta que passa por x 1 , f x 1 e x 2 , f x 2 .

a 1 = f x 2 - f x 1 x 2 - x 1 = 1 - 3 4 - 3 + 1 4 - 2 - 3 - 3 - 2 = - 2 3 4 - 2 3 = 1 4

Agora calculamos o coeficiente angular da reta que passa por x 1 , f x 1 e x 3 , f x 3 ou x 2 , f x 2 e x 3 , f x 3 e verificamos se é 1 4 .

a 2 = f x 3 - f x 1 x 3 - x 1 = 1 - 3 + 1 4 1 - ( 3 - 2 ) = 3 - 3 4 3 - 3 = 1 4

Como os coeficientes angulares são iguais, temos que os 3 pontos são colineares.

Segue um esboço do gráfico com os pontos:

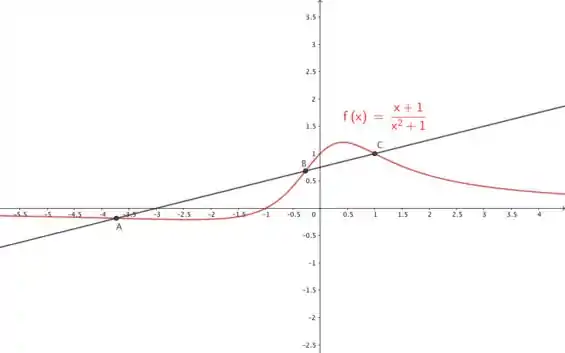
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 16, encontre os pontos de inflexão do gráfico da função dada, se existirem. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfic
Nos Exercícios de 1 a 16, encontre os pontos de inflexão do gráfico da função dada, se existirem. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfic
Nos Exercícios de 17 a 24, ache o ponto de inflexão do gráfico da função dada, se existir. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfico. 2 1
Nos Exercícios de 1 a 16, encontre os pontos de inflexão do gráfico da função dada, se existirem. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfic
Nos Exercícios de 17 a 24, ache o ponto de inflexão do gráfico da função dada, se existir. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfico. 1 9