Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 8

Prove que o pontos A(-4,-1), B(-2,-3), C(4,3) e D(2,5) são vértices de um retângulo.

Passo 1

Pra resolver essa questão, vamos começar marcando os pontos num gráfico, pra ver que tipo de quadrilátero é possível se formar.

Depois, pra gente confirmar que é um retângulo, temos que ver se as retas do comprimento são paralelas, se as retas da largura são paralelas também e se as retas de comprimento e de largura são perpendiculares entre si. Fez sentido? Pra isso a gente vai analisar a inclinação das retas... Vamos começar!

Marcando os pontos no gráfico temos isso aqui:

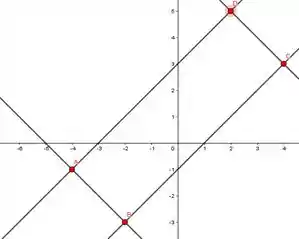
Já tá com cara de retângulo, mas precisamos confirmar!

Passo 2

Para que o quadrilátero seja uma retângulo é preciso que a reta AB seja perpendicular as retas AD e BC e seja paralela à reta CD (o que garante que a reta CD também é perpendicular às retas AD e BC). Vamos, então, determinar o coeficiente angular(inclinação) de cada uma das retas.

Sejam mAB, mAD, mBC e mCD os coeficientes angulares das retas AB, AD, BC e CD, respectivamente. Calculamos eles como m = ∆ y ∆ x .

Na nossa figura temos:

mAB = - 1 - - 3 - 4 - - 2 ⇒

mAB = - 2 2 ⇒

mAB = -1

mAD = 5 - - 1 2 - ( - 4 ) ⇒

mAD = 6 6 ⇒

mAD = 1

.

mBC = - 3 - 3 - 2 - 4 ⇒

mBC = - 6 - 6 ⇒ mBC = 1

mCD = 3 - 5 4 - 2 ⇒

mCD = - 2 2 ⇒

mCD = -1

Passo 3

Observe como mAB = mCD, temos que as retas AB e CD são paralelas.

Agora, fazendo mAB x mAD = -1 e mAB x mBC= -1, vemos que as retas AD e BC são perpendiculares a reta AB.

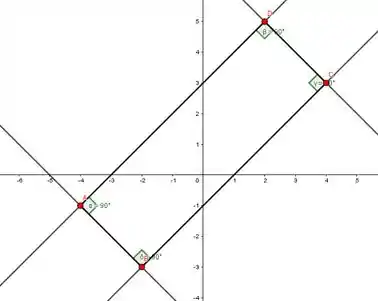
Resposta

Os pontos A, B, C e D formam um retângulo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Mostre que os planos 2 x - y + z = 0 e x + 2 y - z = 1 se interceptam segundo uma reta r; (b) Ache equações da reta que passa pelo ponto A = (1, 0, 1) e intercepta a reta r ortogonalmente.
Achar as equações da reta que intercepta as retas r 1 e r 2 e é perpendicular a ambas. r 1 :x = 1 + t y = 2 + 3 t z = 4 t , t ∈ R r 2 :x + 1 = y - 1 2 = z + 2 3
Seja r a reta determinada pela interseção dos planos x + y - z = 0e2 x - y + 3 z - 1 = 0 . Ache a equação do plano que passa por A = (1, 0, −1) e contem a reta r.
Achar as equações da reta que intercepta as retas r 1 e r 2 e é perpendicular a ambas.b) x = - 1 + t y = 2 + 3 t z = 4 t,t ∈ R r 2 : x = y - 4 2 = z - 3 3
Sejam r e s retas reversas passando por A = (0, 1, 0) e B = (1, 1, 0) e por C = (−3, 1, −4) e D = (−1, 2, −7), respectivamente. Obtenha uma equação da reta concorrente com r e s e paralela ao vetor V