Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 13
Prove que os pontos A(6,-13), B(-2,2), C(13,10) e D(21,-5) são vértices de um quadrado. Ache o comprimento de uma diagonal.
Passo 1
Inicialmente vamos marcar os pontos no plano cartesiano e fazer um esboço da figura geométrica forma por eles.
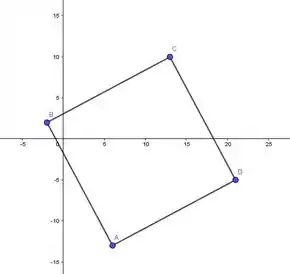
Passo 2
Inicialmente precisamos verificar se a reta que passa pelos pontos A e B é perpendicular à reta que passa por A e D e também a reta que passa por B e C. Para isso, vamos determinar a inclinação das retas que passam por cada lado do quadrilátero.
Inclinação da reta que passa pelo lado AB:
Inclinação da reta que passa pelo lado AD:
Inclinação da reta que passa pelo lado BC:
Inclinação da reta que passa pelo lado CD:
Observe que
O que garante que o segmento AB é perpendicular ao segmento AD e ao segmento BC.
Por outro lado, temos que o que garante que o segmentos AB e CD são paralelos. Assim garantimos que nosso quadrilátero é um retângulo (os quatro ângulos internos medem 90◦)
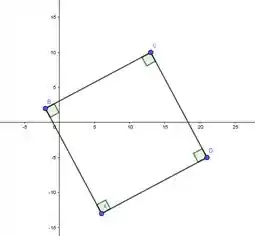
Passo 3
Para que o quadrilátero ABCD seja um quadrado é preciso que seus quatro lados tenham a mesma medida, ou seja, AB = BC = CD = DA. Vamos determinar a medida de cada lado.
AB = 17
Como , temos que o quadrilátero ABCD é um quadrado, como queríamos mostrar.
Passo 4
Agora vamos achar a diagonal desse quadrado! Pra isso temos que lembrar que a diagonal forma um triângulo retângulo com dois lados do quadrado! Assim só temos que usar o teorema de Pitágoras
Como já vimos que o lado do quadrado é
Feshow? :D
Resposta
Demonstração acima
Diagonal: