Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 50

Prove, usando inclinações, que os três pontos A(3, 1), B(6, 0) e C(4, 4) são vértices de um triângulo retângulo e determine a área do triângulo.

Passo 1

Inicialmente devemos verificar se os três pontos não são colineares. Para isso vamos comparar a inclinação das retas que contém cada par de pontos.

→ Inclinação da reta que contém os pontos A e B:

m A B = 0 - 1 6 - 3 ⇒

m A B = - 1 3 ⇒

m A B = - 1 3

→ Inclinação da reta que contém os pontos B e C:

m B C = 4 - 0 4 - 6 ⇒

m A B = 4 - 2 ⇒

m A B = - 4 2 ⇒

m A B = - 2

→ Inclinação da reta que contém os pontos C e A:

m C A = 1 - 4 3 - 4 ⇒

m C A = - 3 - 1 ⇒

m C A = 3

Como m A B ≠   m B C ≠ m C A , temos que os três pontos não são colineares, portanto formam um triângulo.

Passo 2

Observe que

m A B . m C A = - 1 3 . 3 = - 1

Logo os segmentos AB e CA são perpendiculares, o que garante que o triângulo ABC é retângulo.

.

Passo 3

Vamos marcar os pontos A(3, 1), B(6, 0) e C(4, 4) no plano cartesiano e fazer o esboço do triângulo.

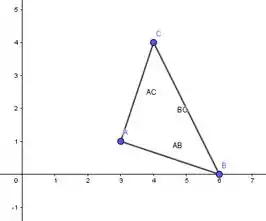
Observe que o triângulo ABC tem como base o segmento AB e como altura o segmento AC. Logo a área do triângulo será dada por

A t = A B . A C 2

Devemos, agora, calcular o tamanho de cada um desses segmentos.

A B = 6 - 3 2 + 0 - 1 2 ⇒

A B = 3 2 + - 1 2 ⇒

A B = 9 + 1 ⇒

A B = 1 0

A C = 4 - 3 2 + 4 - 1 2 ⇒

A C = 1 2 + 3 2 ⇒

A C = 1 + 9 ⇒

A C = 10

Logo,

A t = A B . A C 2 ⇒

A t = 10 . 10 2 ⇒

A t = 10 . 2 2 ⇒

A t = 10 2 ⇒

A t = 5

Resposta

Portanto a área do triângulo é 5.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular o valor de m para que sejam concorrentes as seguintes retas:a) r 1 = y = 2 x - 5 z = - x + 2 e r 2 = x - 5 = y m = z + 1
Calcular o valor de m para que sejam concorrentes as seguintes retas:b) r 1 = x = m - t y = 1 + t z = 2 t e r 2 : x - 1 3 = y + 2 1 = z - 2
Dadas as retas r 1 = x - 1 2 = - y ; z = 3 e r 2 = x = t y = - 1 + t z = 2 + t Encontrar equações reduzidas na variável x da reta que passa por ( 0,1 , 0 ) e pelo ponto de interseção de r 1 com r 2 :
Determine na reta r = x = 2 + t y = t z = - 1 + 2 t Um ponto equidistante do ponto A=( 2 , - 1 , - 2 ) e B = ( 1,0 , - 1 ) .
Determine os pontos da reta r : x = 2 + t , y = 1 + 2 t ,z = 3 + 2 t que:Distam 6 unidades do ponto A = 2,1 , 3 ;