Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.2 - Ex. 20
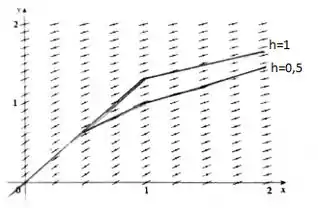
Um campo de direções para uma equação diferencial é apresentado. Desenhe, com uma régua, os gráficos das aproximações de Euler para a curva solução que passa pela origem. Use os passos . As estimativas de Euler estarão superestimadas ou subestimadas? Explique.
Passo 1
Um tamanho de passo menor é uma melhor aproximação de uma função. Como o valor da plotagem com é menor que o valor de , isso implica que o valor real da função deve ser menor que o valor aproximado. Portanto, as estimativas de Euler são superestimadas.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use o campo de direções III para esboçoar os gráficos das soluções que satisfazem as condições iniciais dadas.a) y 0 = 1 b) y 0 = 0 c) y 0 = - 1
Encontre uma equação da(s) tangente(s) à curva no ponto dado. Então, plote a curva e a(s) tangente(s). x = s e nt ,y = s e n( t + s e nt ) , 0 ,0
Encontre uma equação da(s) tangente(s) à curva no ponto dado. Então, plote a curva e a(s) tangente(s). x = 2s e n2 t ,y = 2s e nt , 3 ,1
Mostre que y = 2 3 e x + e - 2 x é uma solução da equação diferencial y ' + 2 y = 2 e x
Verifique se y =- t cos t- t é uma solução do problema de valor inicial t d y d t =y + t 2 sin t, y π = 0