Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.5 - Ex. 25

Quantos termos da série precisamos adicionar para encontrar a soma parcial com a precisão indicada?

25-

∑ n = 1 ∞ - 2 n n !     e r r o < 0 . 01

Passo 1

A série alternada pode ser representada da seguinte forma:

∑ n = 1 ∞ - 1 n × 2 n n !

Pode não ser tão simples ver que essa série alternada é uma série convergente, para isso vamos fazer os devidos testes a seguinte sequência abaixo:

b n = 2 n n !

Vamos fazer o limite de n tendendo a infinito:

lim n → ∞ ⁡ 2 n n ! = lim n → ∞ ⁡ 2 n × 2 n - 1 × 2 n - 2 … 2 3 × 2 2 × 2 1 = 0 × 0 × 0 … c = 0

Logo essa sequência tende a zero.

Agora vamos ver se: b n + 1 < b n , ou seja se a série é decrescente:

2 n + 1 n + 1 ! < 2 n n !

n ! n + 1 ! × 2 n + 1 2 n < 1

n × n - 1 … × 2 × 1 n + 1 × n … × 2 × 1 × 2 < 1

2 n + 1 < 1

n + 1 > 2 → n > 1

A série é decrescente a partir de n = 1 . O que torna o nosso teste verdadeiro, pois é a partir de n = 1 que a série começa.

Passo 2

Dessa forma cada termo adiciona uma precisão a soma da série de forma que:

2 n n ! < 0 . 01

Essa conta é um tanto quanto complicada de fazer analiticamente, precisando então de métodos numéricos para poder resolver-la

Plotando um gráfico das duas funções nós teremos

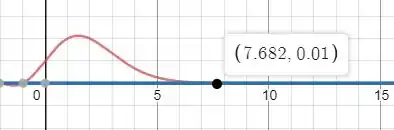
Logo para ser menor que 0.01 temos que ter:

n = 8

Resposta

n = 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Teste a série para convergência ou divergência.8- ∑ n = 1 ∞ - 1 n 2 n 4 n 2 + 1
Quantos termos da série precisamos adicionar para encontrar a soma parcial com a precisão indicada? ∑ n = 1 ∞ - 1 n + 1 n 4 e r r o0.001
Teste a série para convergência ou divergência.4- 1 ln ⁡ 2 - 1 ln ⁡ 3 + 1 ln ⁡ 4 - 1 ln ⁡ 5 + 1 ln ⁡ 6 + …
Teste a série para convergência ou divergência.6- ∑ n = 1 ∞ - 1 n - 1 3 n - 1
Quantos termos da série precisamos adicionar para encontrar a soma parcial com a precisão indicada?26- ∑ n = 1 ∞ - 1 n n 4 n e r r o0.002