8. (a) Para , faça os gráficos de em função de para as soluções com pontos iniciais , e . Use um intervalo para t de, pelo menos,. Compare seus gráficos com os da Figura .
(b) Repita os cálculos do item (a) para e. Aumente o intervalo para o quanto for necessário para que você possa determinar quando cada solução começa a convergir para um dos pontos críticos. Registre a duração aproximada do estado transiente caótica em cada caso. Descreva como essa quantidade depende do valor de .
(c) Repita os cálculos feitos nos itens (a) e (b) para valores de ligeiramente maiores do que . Tente estimar o valor de para o qual a duração do estado transiente caótico tende a infinito.
Passo 1
Para esse item, vamos usar exatamente o mesmo código usado na questão 6 dessa seção. A diferença mais importante vai ser nas definições de variações do tempo (O INTERVALO DO TEMPO) e também das condições iniciais (VALORES INICIAIS):
AHHH! Não se esqueça de mudar o valor de para valores ligeiramente maiores que na definição da função derivada, heim:

Passo 2
USANDO :
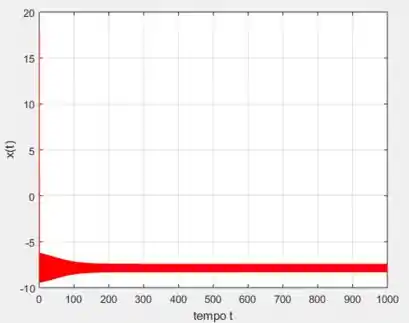
Usando variando no intervalo de e o ponto inicial:
Então, colocando o programa pra rodar, vamos obter...
Mudando o ponto para ...
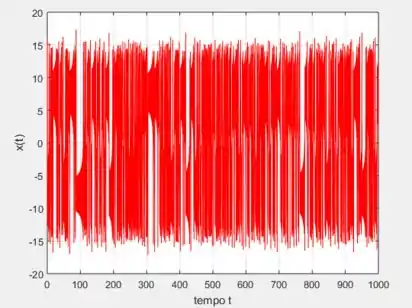
Nesse caso, usei um intervalo maior para o tempo .
Para o ponto inicial :
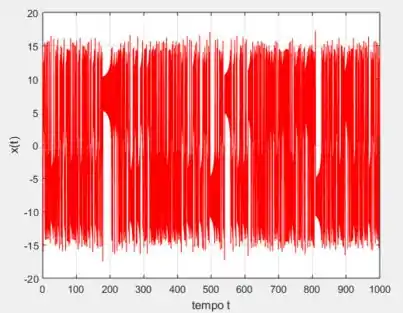
Perceba que de acordo com essas duas últimas, o tempo caótico já é infinito, mas o primeiro ainda tem um tempo finito, mas de convergência bem mais lenta.
Passo 3
USANDO :
Usando variando no intervalo de e o ponto inicial:
Então, colocando o programa pra rodar, vamos obter...
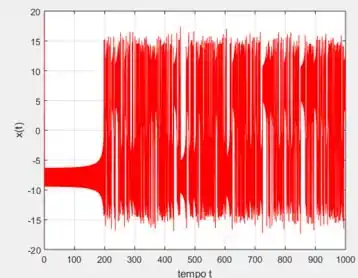
Mudando o ponto para ...
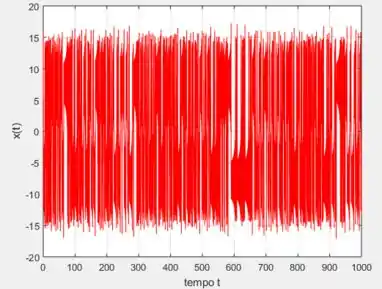
Nesse caso, usei um intervalo maior para o tempo .
Para o ponto inicial :
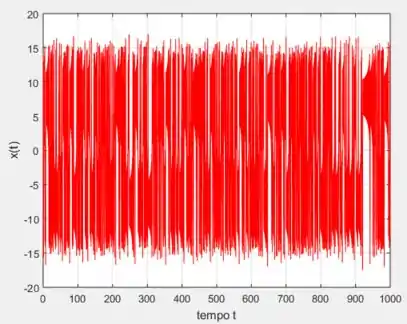
OPA!!! Até mesmo o primeiro gráfico entrou no estágio caótico, o que indica que para , já podemos considerar um tempo caótico infinito.
Te vejo na próxima então!
Resposta
Ei, a resposta está no passo a passo :)