Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.1 - Ex. 1 b
b) Encontre novas estimativas usando 8 retângulos.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar as estimativas inferior e superior para a área sob o gráfico de no intervalo de até , utilizando retângulos.
Pra isso, vamos relembrar que as estimativas superiores e inferiores, em um intervalo são obtidas através da soma:
Onde e .
Como já foi dado o intervalo, temos que e E como é crescente podemos obter uma estimativa inferior usando os pontos da esquerda e os pontos interiores da direita para obter a estimativa superior.
Nós fomos instruídos a usar retângulos, então e como , temos que:
Então, vamos escolher alguns pontos no gráfico e usar a fórmula para obter as estimativas de áreas através da soma dos retângulos.
Vamos lá!
Passo 2
Usando a fórmula, com , vamos fazer a estimativa inferior:
Então, escolhendo alguns pontos do gráfico para fazer uma estimativa inferior, temos:
Desenhando esses retângulos abaixo da curva no gráfico, olha só como fica:
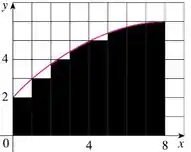
Daí, nós conseguimos extrais os valores de para cada escolhido:
Fazendo essa soma, obtemos a estimativa inferior:
Passo 3
Agora, vamos fazer uma estimativa superior para .
Para a gente fazer menos contas, perceba que a soma dos retângulos superiores é igual a , ou seja:
E como no nosso caso , teremos portanto que:
Fuja de contas meu amigos!
Olha só como fica o gráfico:
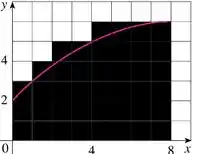
Então, substituindo os valores, temos:
E calculando, obtemos a estimativa superior:
Prontinho, galera! Até a próxima! 😉