Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 8
Avalie as somas superiores e inferiores para , com e 4. Ilustre com diagramas como Figura 14.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente avaliar as somas superiores e inferiores para
No intervalo , com e . E ilustrar tudo isso com o diagrama da figura 14 .
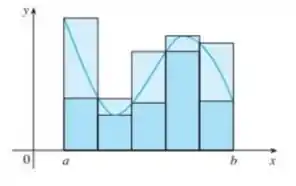
Pra isso, nós precisamos lembrar que:
A área da região S que está sob o gráfico de uma função contínua é a soma das áreas dos retângulos aproximantes:
onde e é definido analisando o gráfico de .
Sendo assim, vamos substituir os dados da função na fórmula do somatório e estimar a área sob o gráfico.
Vamos lá!
Passo 2
Vamos começar esboçando o gráfico da função :
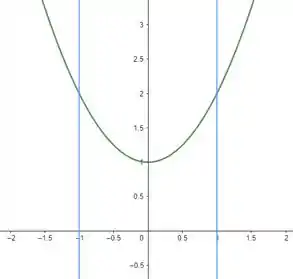
Observe que as linhas em azul estão delimitando nosso intervalo . Agora vamos usar o gráfico para estimar a nossa área.
Agora, vamos calcular a soma superior através de retângulos. Perceba que da nossa fórmula e . Dessa forma, temos:
Como precisamos de 4 retângulos, temos . Daí,
Então, vamos definir os intervalos:
Tranquilo até aqui?
Passo 3
Para encontrar a soma superior, vamos escolher os maiores valores do intervalo.
Como é decrescente em até , corresponde aos extremos da esquerda do intervalo. E a partir de os da direita.
Ou seja .
Substituindo isso na fórmula de área do somatório, temos:
Olhando no gráfico, vamos extrair os valores de :
Que correspondem aos retângulos:
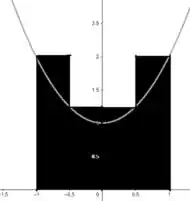
Show?
Passo 4
De modo semelhante, temos para a soma inferior:
Substituindo na fórmula:
E calculando:
Desenhando esses retângulos no gráfico, temos:
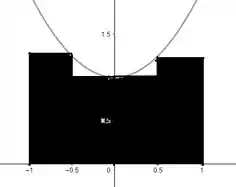
Bacana, não é?
Passo 5
Agora vamos usar 3 retângulos, ou seja, quando . Daí, temos:
Definindo os intervalos:
Vamos achar a soma superior, escolhendo os maiores valores do intervalo.
Como é decrescente em até , corresponde aos extremos da esquerda do intervalo. E a partir de os da direita.
Ou seja:
Substituindo esses pontos na fórmula do somatório, temos:
Olhando no gráfico, pra extrair os :
Que correspondem aos retângulos:
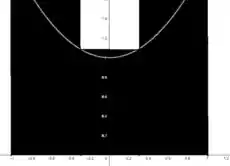
Maravilha!
Passo 6
Da mesma forma, calculando a soma inferior, vamos ter:
Daí, extraindo os valores no gráfico e calculando, temos:
Esboçando o diagrama:
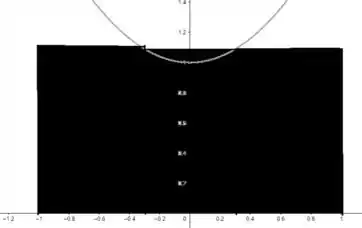
Valeu, galera! Até a próxima! 😉
Resposta
Sendo = Soma superior e = soma inferior, temos:
- Para e
- Para e