Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.4 - Ex. 2
O que é mais razoável esperar: ?
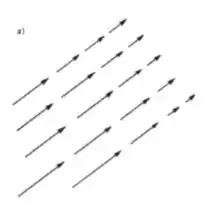
Passo 1
Bom, o divergente mostra uma variação do fluxo no campo vetorial. Tipo, se o divergente for positivo, os vetores vão aumentar de acordo com o tempo. Se for negativo, vão diminuir. E se for nulo, os vetores se mantém da mesma forma com o decorrer do tempo. Ou seja, se o divergente é zero, o fluxo total que “entra” é o mesmo que “sai”.
- Vejamos então a primeira figura. Acompanhe as linhas de vetores. Tá vendo que os vetores estão diminuindo de tamanho? Isso quer dizer que está tendo uma variação de fluxo no decorrer do tempo, ou seja, nesse caso é mais razoável esperarmos que:
- Fazendo o mesmo procedimento na segunda figura, nós vemos que vetores não variam no decorrer do tempo, eles se mantém do mesmo tamanho. Ou seja, nesse caso é mais razoável dizermos que:
Passo 2
Resposta
Exercícios de Livros Relacionados
Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S ( 2 d y d z + 3 d z d x - 5 d x d y ) onde S é a superfície do paraboloide z = 9 - x 2 - y 2 acima do plano z = 0 .
Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S f → ⋅ n → d S Sendo f → = ( 2 x , 2 y , 0 ) e S a superfície do Exercício 13, exceto a face superior.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
Usar o teorema da divergência para calcular a integral da superfície dada. I = ∬ S 4 x - y d y d z + y 2 d z d x - x y d x d y Onde S é a superfície exterior do cubo limitado pelos planos coordenados
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2