Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 44
Um recipiente tem a forma e as dimensões de um sólido de revolução descrito pela rotação da região no primeiro quadrante, limitada pela parábola ,pelo eixo e pela reta , em torno do eixo . Se o recipiente estiver cheio de água, ache o trabalho realizado para se bombear toda água até um ponto 3p acima da borda do recipiente m acima da borda do recipiente. Tome a aceleração da gravidade igual a 10 m/s.
Passo 1
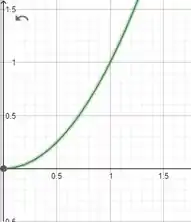
Escolheremos o eixo como nos eixos cartesianos, positivo para cima e positivo para direita.
Iremos escolher uma partição do intervalo de . E para vermos a soma de Riemann, teremos um ponto qualquer no subintervalo .
Apenas um comentário sobre o que escrevemos acima, não liga muito para a formalidade, pense nesse intervalo como dois pontos de alturas distintas. Melhorou né!
Passo 2
Agora vamos imaginar um pouquinho! Pensa num elemento muito fino, vamos apelida-lo de elementinho, a sua espessura será:
Esse elementinho será um disco circular com centro no eixo , seu raio será , o volume do elementinho é:
E pensaremos no peso do elementinho, chamaremos de o peso de 1 kg de água, então o peso do elementinho será:
Passo 3
Já temos o peso, teremos que calcular a distância, lembrando que a posição do ponto, quando é muito próximo de , é igual a .
Qual seria a distância percorrida? Ora, é a distância do fundo do recipiente menos a posição do objeto:
Quando é a posição em , temos que:
Voltando para o nosso elementinho, faremos o volume e o trabalho em função de
Pensando em todos os elementinhos teremos:
Para finalizar! Já estava na hora né, calcularemos essa integral:
Lembrando , temos: