Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.6 - Ex. 2

Com referência ao exemplo 1.

  1. Ache a sequência da reta tangente à curva y = 1 / t que é para paralela à reta secante A D .
  2. Use a parte ( a ) para mostrar que ln ⁡ 2 > 0,66 .

Passo 1

O exemplo 1 nos diz que ln ⁡ x = ∫ 0 x 1 t d t   com x > 0 . Além disso nos dá a seguinte imagem

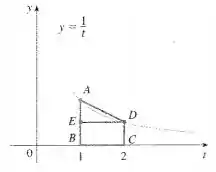
Dada a nossa curva y = 1 t → y ' = - 1 t 2 . A inclinação de A D é dada por

1 2 - 1 2 - 1 = - 1 2

Tomemos, então, um ponto c tal que c seja um ponto na curva dada cuja inclinação seja - 1 2 . Sendo assim, teremos

- 1 c 2 = - 1 2 → c = 2 ,   c > 0

Portanto, a reta tangente será dada por

y - 1 2 = - 1 2 ⋅ t - 2 → y = - t 2 + 2

Passo 2

Como nosso gráfico é côncavo para cima, o gráfico fica acima da linha tangente, ou seja, acima do segmento de linha B C . Agora, temos alguns valores importantes em módulo que nos serão úteis

A B = - 1 2 + 2   e   C D =   - 1 + 2

Assim, a área do trapézio ABCD é

1 2 ⋅ - 1 2 + 2 + - 1 + 2 ⋅ 1 ≈ 0,6642

Sendo assim, podemos fazer a seguinte desigualdade

ln ⁡ 2 > Á r e a   d o   t r a p é z i o   A B C D > 0,66

Resposta

( a ) y = - t 2 + 2

b ln ⁡ 2 > 0,66 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça uma crítica da “demosntração” seguinte de que toda constante de integração é nula. C = ∫ 0d x = ∫ 0 ⋅ 0d x = 0 ∫ 0d x = 0
Os campos de direções dados correspondem a uma das equações diferenciais abaixo. Identifique a equação diferencial que combina com a figura e esboce curvas e soluções pelos pontos destacados.
Os campos de direções dados correspondem a uma das equações diferenciais abaixo. Identifique a equação diferencial que combina com a figura e esboce curvas e soluções pelos pontos destacados.
Encontre uma equação da curva que satisfaz as condições dadas.Em cada ponto ( x ,y ) da curva, y satisfaz a condição d 2 y / d x 2 = 6 x ; a reta y = 5 - 3 x é tangente à curva no ponto onde x = 1 .
Os campos de direções dados correspondem a uma das equações diferenciais abaixo. Identifique a equação diferencial que combina com a figura e esboce curvas e soluções pelos pontos destacados.