Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.3 - Ex. 32
A região entre a curva e a reta gira em torno da reta . Use camadas cilíndricas para encontrar o volume do sólido resultante. (Suponha
Passo 1
E aí, tudo joia?
Vamos começar dando uma olhada em como seria o gráfico disso?
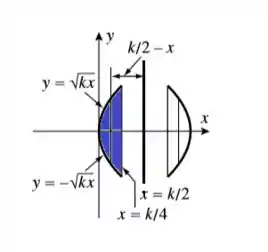
Olha só, a parte em azul é a região que vai gerar o sólido (a outra parte é só a projeção dela). A gente vai girar essa parte em torno da reta . E daí a gente pode montar nossa integral, lembrando que:
Passo 2
Como as funções são simétricas, a gente pode usar pra calcular o volume apenas , já que são duas partes iguais.
Vamos usar cascas cilíndricas pra calcular o volume, ou seja, vamos usar a fórmula:
No nosso caso a integral fica:
Integral montada, agora a gente vai calcular...
Passo 3
Resolvendo:
E prontinho! Esse é o volume😉
Resposta
Exercícios de Livros Relacionados
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = 2 x - x 2 , y = 0
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.A aproximação das somas de Riemann V ≈ ∑ k = 1 n 2 π x k nf x k n Δ x ko n d ex k n = x k + x k - 1 2 para o volume de um sól
( a ) Use camadas cilíndricas para encontrar o volume do sólido que é gerado quando a região sob a curva y = x 3 - 3 x 2 + 2 x e acima de [ 0 ,1 ] gira em torno do eixo y . ( b ) Para esse problema, o
Usando o método das camadas cilíndricas, monte uma integral (mas não a calcule) para o volume do sólido gerado quando a região R é girada em torno ( a ) da reta x = 1 e ( b ) da reta y = - 1 . R é a r
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.No método das camadas cilíndricas, a integração é efetuada num intervalo do eixo de coordenadas que é perpendicular ao eixo d