Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.3 - Ex. 34

Use camadas cilíndricas para encontrar o volume do toro obtido fazendo girar o círculo x 2 + y 2 = a 2 em torno da reta x = b , sendo b > a > 0 . [Sugestão: pode ajudar na integração imaginar que a integral é uma área.]

Passo 1

Olá, tudo bem?

Vamos começar dando uma olhada em como seria o gráfico disso?

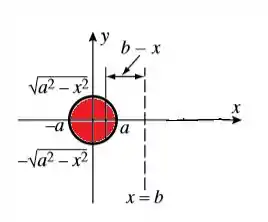
O toro que a gente quer saber o volume é o resultado da rotação do círculo em vermelho em torno da reta x = b pontilhada ali.

O círculo está centrado na origem, sendo que a parte debaixo é representada por y = - a 2 - x 2 e a de cima por y = a 2 - x 2 .

Como as duas partes são iguais, podemos considerar só uma e multiplicar por dois.

Passo 2

Tendo feito essas observações, vamos montar a integral do volume:

V = ∫ - a a 2 π b - x 2 a 2 - x 2   d x

V = ∫ - a a 4 π b - 4 π x a 2 - x 2 d x

Vamos separar assim agora:

V = 4 π b ∫ - a a a 2 - x 2   d x - 4 π ∫ - a a x a 2 - x 2   d x  

Essa primeira integral é a área do semicírculo de raio a , então:

∫ - a a a 2 - x 2   d x = π a 2 2

Passo 3

Vamos ver a outra integral agora:

∫ - a a x a 2 - x 2   d x = - a 2 - x 2 3 2 3 - a a = 0

Juntando essas informaçõeszinhas, temos:

V = 4 π b π a 2 2 -   4 π ( 0 )

V = 2 π 2 b a 2

E conseguimos! Esse é o volume😉

Resposta

V = 2 π 2 b a 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo x . y 2 = x , y = 1 , x = 0
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo x . y = x 2 , x = 1 , y = 0
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo x . x y = 4 , x + y = 5
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo x . x = 2 y , y = 2 , y = 3 , x = 0