Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 51

A região de x = 0 a x = π 2 limitada pela curva y = s e n   x , pela reta y = 1 e pelo eixo y gira em torno do eixo x . Ache o volume do sólido gerado.

Passo 1

A questão pede o volume gerado pela rotação da região mostrada na figura a seguir em torno do eixo x .

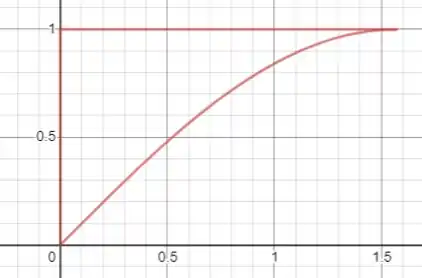
Para acharmos esse volume vamos fazer uma integral na variável x de x = 0 até x = π / 2 . A raio inferior é y = s e n   x , enquanto o superior é y = 1 . Assim, o volume será

V = π ∫ 0 π 2 1 2 - s e n   x 2   d x = π ∫ 0 π 2 1 - s e n 2 x   d x

Passo 2

Para calcular essa integral você precisa lembrar que

s e n 2 x = 1 2 - 1 2 cos ⁡ 2 x

Assim,

1 - s e n 2 x = 1 2 + 1 2 cos ⁡ 2 x

Portanto, o volume será

V = π 2 ∫ 0 π 2 1 + cos ⁡ 2 x   d x

Fazendo a mudança de variável t = 2 x , temos que d x = d t / 2 :

V = π 4 ∫ 0 π 1 + cos ⁡ t   d t

Passo 3

Fazendo a integral:

V = π 4 t + s e n   t 0 π = π 4 ⋅ π

Portanto,

V = π 2 4

Resposta

π 2 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido S descrito.A base de S é um disco circular de raio r . Secções transversais paralelas, perpendiculares à base, são quadradas.
Escreva uma integral para um toro sólido (o sólido com formato de rosquinha da figura) com raios r e R .Interpretando a integral como uma área, encontre o volume do toro.
Ache o volume comum aos dois cilindros circulares, cada qual com raio r , se os eixos dos cilindros se interceptam em ângulos retos.
Um buraco de raio r é perfurado pelo centro de uma esfera de raio Rr . Encontre o volume da porção remanescente da esfera.