Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 63

  1. Escreva uma integral para um toro sólido (o sólido com formato de rosquinha da figura) com raios r e R .
  2. Interpretando a integral como uma área, encontre o volume do toro.

Passo 1

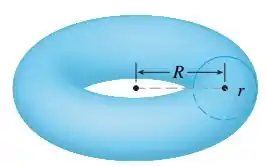
A questão nos dá a seguinte figura que trata-se de um toro sólido (um sólido com formato de rosquinha):

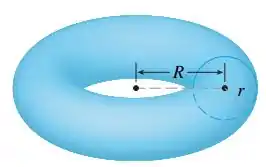
Queremos escrever a integral para o toro sólido com raios r e R .

Além disso, devemos encontrar o seu volume tratando a integral que iremos descobrir como uma área.

Para resolvermos isso, temos que observar que esse sólido trata-se de um sólido de rotação.

Onde podemos determinar o volume V da seguinte forma:

V = π ∫ a b y 2   d x

Passo 2

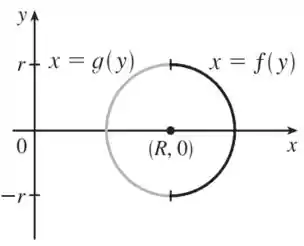
O toro é obtido pela rotação da circunferência x - R 2 + y 2 = r 2 pelo eixo y .

Temos que o lado direito da circunferência é dado por x = R + r 2 - y 2 = f y e o lado esquerdo por x = R - r 2 - y 2 = g y :

Passo 3

Vamos ter então que o volume é dado pela equação abaixo, com os limites de integração sendo os extremos da circunferência, a = - r e b = r :

V = ∫ a b π A y d y ∴

V = π ∫ - r r f y 2 - g y 2 d y ∴

V = π ∫ - r r R + r 2 - y 2 2 - R - r 2 - y 2 2 d y ∴

V = π ∫ - r r R 2 + 2 R r 2 - y 2 + r 2 - y 2 - R 2 - 2 R r 2 - y 2 + r 2 - y 2 d y ∴

V = π ∫ - r r 4 R r 2 - y 2 d y ∴

V = 4 R π ∫ - r r r 2 - y 2 d y ∴

V = 8 R π ∫ 0 r r 2 - y 2 d y

Passo 4

Pela figura da pra perceber que a integral representa um quarto de área de uma circunferência de raio r , assim:

V = 8 R π ∫ 0 r r 2 - y 2 d y ∴

V = 8 R π 1 4 π r 2 ∴

V = 2 π 2 r 2 R

Prontinho!

Resposta

  1. V = 8 R π ∫ 0 r r 2 - y 2 d y
  2. V = 2 π 2 r 2 R
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = cos ⁡ x 2 , x = 0 , x = 1 2 π , y = 0
Sejam R 1 e R 2 regiões com a forma mostrada abaixo. Use camadas cilíndricas para encontrar o volume do sólido que resulta quando ( a ) a região R 1 gira em torno do eixo y . ( b ) a região R 2 gira e
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = e x 2 , x = 1 , x = 3 , y = 0
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = 1 / x , y = 0 , x = 1 , x = 3
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.