Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 18
Calcule o valor da integral múltipla.
Passo 1
E aí meus queridxs, tudo bom com vocês? Vamos lá, precisamos calcular a integral acima de acordo com a região dada. Para isso, vamos primeiramente reescrever nossa integral de forma que ela possa ser escrita como uma integral iterada. Ou seja, temos que montar essa integral com os limites de integração corretamente. Veja os vértices que temos de uma região triangular, perceba que vai de a .
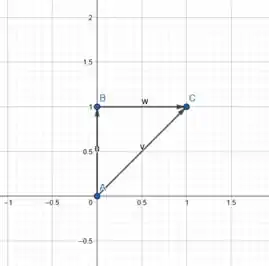
Perceba que varia linearmente com então, tomemos a região de integração dada por:
Então temos:
Passo 2
Beleza, agora que temos nossa integral escrita de forma iterada podemos calcular seu valor de forma bem tranquila, vindo de ‘dentro pra fora’ e enquanto resolvemos uma integral em uma variável consideraremos tudo o que não for essa variável como constante. Dessa forma, temos
Resolvendo a integral mais interna vamos ter
Agora, ficamos com a seguinte integral simples a ser resolvida
Para resolver a segunda integral vamos utilizar a seguinte substituição simples:
, assim, obteremos
Integrando
Aplicando os limites de integração:
Pronto, tá resolvido nosso exercício sem muitos problemas.