Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 50

A região limitada pelas curvas y = tan ⁡ x e y = cot ⁡ x e pelo eixo x , onde 0 ≤ x ≤ π 2 , gira em torno do eixo x . Ache o volume do sólido obtido.

Passo 1

A questão pede o volume obtido pela rotação da região limitada pelas curvas y = tan ⁡ x , y = cot ⁡ x e a reta y = 0 em torno do eixo x .

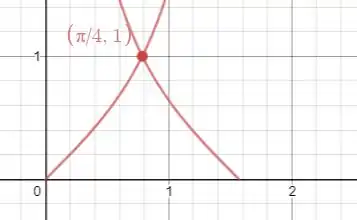
Para calcular esse volume nós temos que quebrar em duas integrais: uma de 0 até π / 4 e outra de π / 4 até π / 2 . Na primeira, o “raio” é y = tan ⁡ x , enquanto na segunda é y = cot ⁡ x . Assim, o volume será

V = π   ∫ 0 π 4 tan 2 ⁡ x   d x + ∫ π 4 π 2 cot 2 ⁡ x   d x

Passo 2

Vamos precisar das primitivas de tangente ao quadrado e cotangente ao quadrado nessa questão. Para a tangente, lembre-se que

1 + tan 2 ⁡ x = sec 2 ⁡ x ⇒ tan 2 ⁡ x = sec 2 ⁡ x - 1

Assim,

∫ tan 2 ⁡ x   d x = ∫ sec 2 ⁡ x - 1   d x = tan ⁡ x - x + C

Analogamente,

cot 2 ⁡ x + 1 = csc 2 ⁡ x ⇒ cot 2 ⁡ x = csc 2 ⁡ x - 1

Portanto,

∫ cot 2 ⁡ x   d x = ∫ csc 2 ⁡ x - 1   d x = - cot ⁡ x - x + C

Vamos usar essas primitivas para calcular o volume!

Passo 3

Agora que sabemos as primitivas, temos que

V = π   ∫ 0 π 4 tan 2 ⁡ x   d x + ∫ π 4 π 2 cot 2 ⁡ x   d x = π   tan ⁡ x - x 0 π / 4 + π - cot ⁡ x - x π / 4 π / 2

Portanto,

V = π   1 - π 4 - 0 + 0 - 0 + π 2 - 1 - π 4

Logo,

V = π 1 + 1 - π 4 - π 2 + π 4 = π 2 - π 2

Resposta

π 2 - π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido S descrito.Uma pirâmide com altura h e base triangular equilátera com lado a (um tetraedro).
O sólido está situado entre planos perpendiculares ao eixo x em x = 0 e x = 4 . As seções transversais são quadrados cujas diagonais se estendem da parábola y = x a y =- x . Determine o volume do sóli
Ache, pelo corte, o volume de um tetraedro com três faces mutuamente perpendiculares e três arestas mutuamente perpendiculares cujos comprimentos são a , b e c unidades.
A torre de uma igreja tem 30m de altura e toda secção horizontal plana é um quadrado, sendo o comprimento dos lados igual a um décimo da distância da secção plana ao topo da torre. Ache o volume da to
A região de x = 0 a x = π 2 limitada pela curva y = s e nx , pela reta y = 1 e pelo eixo y gira em torno do eixo x . Ache o volume do sólido gerado.