Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 47
A torre de uma igreja tem de altura e toda secção horizontal plana é um quadrado, sendo o comprimento dos lados igual a um décimo da distância da secção plana ao topo da torre. Ache o volume da torre.
Passo 1
A questão pede o volume de uma torre cujo formato é uma pirâmide base retangular. Um corte transversal de metade da pirâmide é mostrado na figura a seguir:
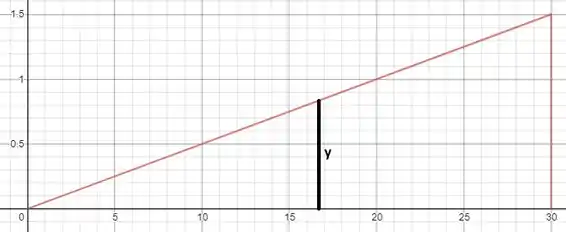
Na figura, representa metade do lado de secção horizontal. Sabemos que a medida do lado do quadrado é um décimo da distância ao topo da torre, representada por :
Assim, a área da secção horizontal será
Para achar o volume basta integrar essa área de até :
Passo 2
Assim, temos que
Fazendo a integração:
Assim, o volume será
Resposta
Exercícios de Livros Relacionados
Um buraco de raio r é perfurado pelo meio de um cilindro de raio Rr com ângulo reto em relação ao eixo do cilindro. Encontre, mas não calcule, uma integral para o volume cortado.
Seja V o volume do sólido obtido pela rotação em torno do eixo y da região limitada por y = x e y = x ² ². Encontre V pelo método de fatiamento e cascas cilíndricas. Em ambos os casos, desenhe um diag
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Explique por que é complicado usar fatias para encontrar o volume V de S . Esboce uma casca de aproximação tí
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume