A região limitada por um pentágono com vértices em , , , e gira em torno do eixo . Ache o volume do sólido gerado.

A questão pede o volume de um sólido de revolução obtido ao girarmos em torno do eixo o pentágono limitado pelos pontos , , , e :

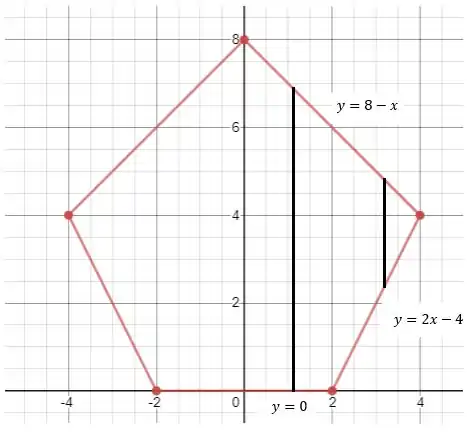
A integração deveria ser feita sobre todo o pentágono, de até . Todavia, note que a figura é simétrica, de modo que só precisamos fazer a integração de até e colocar um fator na frente!

Na figura estão indicadas as equações das retas que serão úteis no cálculo do volume. Note que a reta passa pelos pontos e , a reta passa pelo ponto e e a reta passa pelos pontos e .

Para calcularmos o volume teremos que quebrar a integral em duas: uma de até e outra de até . Na primeira integral temos que o raio inferior é e o raio superior é . Assim, ela será

Já na segunda integral, a raio inferior é e o superior continua sendo :

Assim, o volume todo será

Não esqueça desse fator na frente!