Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 1

1. Deduza a fórmula para o volume de uma esfera de raio r unidades por meio de um corte.

Passo 1

Para esta demonstração utilizamos o conceito de integral definida. Vamos supor a circunferência abaixo com centro na origem:

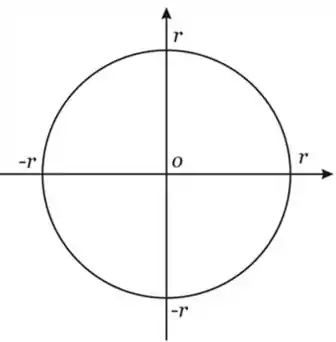
Se rotacionarmos a circunferência em torno do eixo x , obteremos uma esfera de centro na origem e raio r .

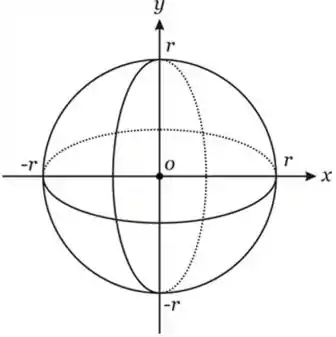
Temos que a equação da circunferência com o raio na origem é:

x 2 + y 2 = r 2

Logo:

y = r 2 - r 2

Passo 2

Para encontrarmos o volume desta esfera, vamos supor fatias de larguras infinitesimais d x e raio y .

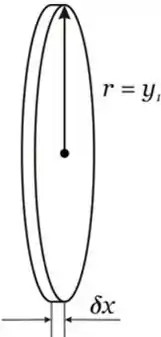
O volume do cilindro é dado por:

V = A b ⋅ h

V = π r 2 ⋅ h

Como o raio do cilindro de altura infinitesimal é igual a d x e seu raio da base é igual a y , podemos reescrever a fórmula do seu volume como:

V = π y 2 d x

Podemos dizer que a esfera é formada por infinitos cilindro de alturas infinitesimais d x , onde seu raio y é variável para cada cilindro.

A soma desses cilindros de alturas infinitesimais é dado pela integral definida:

V = ∫ - r r π y 2 d x

V = π   ∫ - r r y 2 d x

Como:

y = r 2 - x 2

Temos:

V = π ∫ - r r r 2 - x 2 2 d x

V = π ∫ - r r r 2 - x 2 d x

V = π r 3 x - x 3 3 - r r

V = π r 2 r - r 3 3 - r 2 - r - - r 3 3

V = π r 3 - r 3 3 - - r 3 + r 3 3

V = π 2 r 3 - 2 r 3 3

V = 4 3 π r 3

Resposta

V = 4 3 π r 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3 - O sólido está situado entre os planos perpendiculares ao eixo x em x = π 4 e x = 5 π 4 As seções transversais entre esses planos são discos circulares cujos diâmetros vão da curva y = 2 cos ⁡ x à
Nos Exercícios 1-10, determine os volumes dos sólidos.5- A base de um sólido é a região entre a curva y = 2 sen ⁡ x e o intervalo [ 0 , π ] no eixo x . As seções transversais perpendiculares ao eixo x
Nos Exercícios 1-10, determine os volumes dos sólidos.5- A base de um sólido é a região entre a curva y = 2 sen ⁡ x e o intervalo [ 0 , π ] no eixo x . As seções transversais perpendiculares ao eixo x
Nos Exercícios 1-10, determine os volumes dos sólidos.8- A base de um sólido é a região limitada pelos gráficos de y = x e y = x / 2 . As seções transversais perpendiculares ao eixo x são: Triângulo i
Nos Exercícios 1-10, determine os volumes dos sólidos.3- O sólido está situado entre planos perpendiculares ao eixo x em x = - 1 e x = 1 . As seções transversais perpendiculares ao eixo x entre esses