Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 1
Nos Exercícios 1-8, descreva a região dada em coordenadas polares.
Passo 1
Faaaala, cara! Tranquileba?
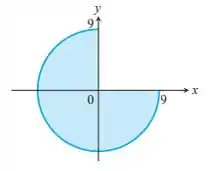
Temos uma circunferência. Sabendo das circunferências que a equação é dada pelo tipo . Partir disto, basta-nos fazer as mudanças de coordenadas.
Passo 2
Sabemos pelas coordenadas polares que:
E temos dado na figura que r=9, e também vemos que o ângulo que chamamos de percorre de
Resposta
Exercícios de Livros Relacionados
Use coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 6 - x 2 - y 2 e z = 2 x 2 + 2 y 2 .
Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 2 ∫ 0 2 x - x 2x 2 + y 2 d y d x
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste para oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade nor
Uma região R é mostrada. Decida se você deve usar coordenadas polares ou retangulares, e escreva ∬ R f x , y d A como uma integral iterada, onde f é uma função qualquer contínua em R .
Use coordenadas polares para determinar o volume do sólido dado.Acima do cone z = x 2 + y 2 e abaixo da esfera x 2 + y 2 + z 2 = 1 .