Faça o gráfico das duas soluções básicas da equação diferencial e de várias outras soluções. Que aspecto têm em comum as suas soluções?

14-

A solução de uma EDO de segunda ordem com raízes reais e distintas e domínio em é:

Substituindo as raízes que encontramos no passo anterior nós teremos:

Isso nos abre uma família de gráficos basta arbitrar valores de e de .

A melhor forma de ver isso é pelo link a seguir e ficar alterando os valores de e de pelo slider:

https://www.desmos.com/calculator/zvpltg7dz1

Caso não dê para ver (só digitar no navegador) temos a seguinte foto abaixo:

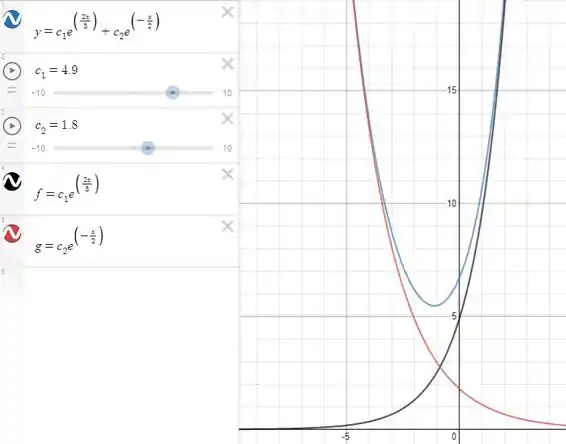
Que nos mostra que a solução é limitada lateralmente pelas duas soluções que a compõem e que tem assíntotas em .

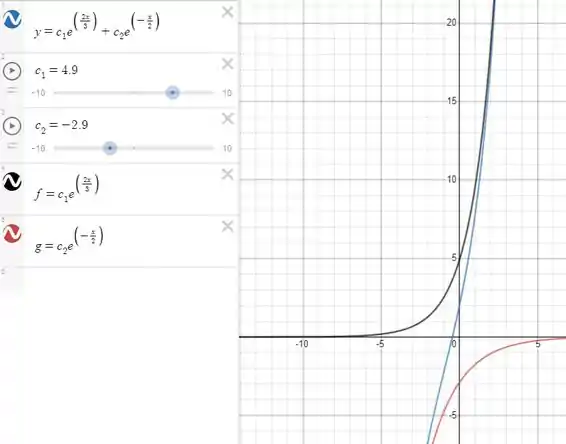
Mesmo quando um dos valores é negativo.

O ponto é, toda solução com raízes reais e distintas nos dá com a questão é o sinal de ou de