Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 2
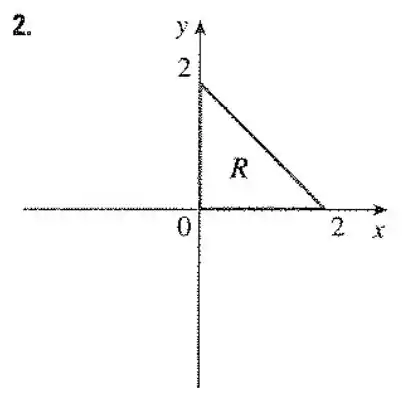
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma arbitrária qualquer contínua em .
2-
Passo 1
Fala pessoal, o exercício nos pede para montar uma integral iterada da região abaixo:
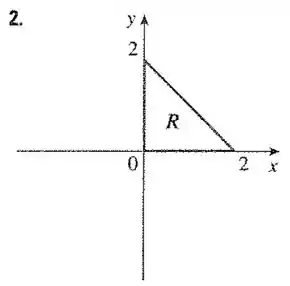
Podemos representar a integral do tipo 1 da seguinte forma:
Onde R :
Para montá-la vamos precisar encontrar algumas informações. A primeira é qual tipo de coordenadas iremos usar. Como se trata de segmentos de retas, a melhor opção é utilizar coordenadas cartesianas.
A segunda informação é saber quem são os limites de integração , ou seja, quanto vão poder variar. Para isso, vamos precisar achar a equação da reta e analisar o gráfico.
Com essas informações poderemos montar a nossa integral, vamos lá?
Passo 2
Vamos come��ar encontrando a equação da reta através da equação :
Para isso precisamos achar os dois pontos pertencentes a essa reta, que o exercício nos dá através da figura .
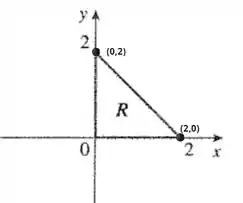
Substituindo os pontos na fórmula, sabemos que :
como sabemos que
Logo a reta será:
Passo 3
Agora vamos analisar os limites de integral, começando por x . Podemos ver pelos pontos : e , que os seu menor valor será e seu maior valor será (. Sendo assim :
Agora vamos analisar o . Acabamos de descobrir que ele varia de acordo com o valor de como vimos na fórmula :
ou
Ou seja, como ele depende de seu valor máximo será a função , já o seu menor valor corresponderá a zero , isso ocorre quando .
Agora vamos substituir os limites de integração :
Lembrando que essa integral com coordenada cartesiana é do tipo 1. E aqui faz diferença quem vem primeiro, como é do tipo 1 então terá alguma dependência com . Poderia se utilizar o tipo 2 (linhas horizontais) sem problema, também.
Resposta
Coordenada cartesiana.